● 텐서플로우(Tensorflow) 기초
- 가장 널리 쓰이는 딥러닝 프레임워크 중 하나
- 구글이 주도적으로 개발하는 플랫폼
- 파이썬, C++ API를 기본적으로 제공,
자바스크립트, 자바, 고, 스위프트 등 다양한 프로그래밍 언어를 지원 - tf.keras를 중심으로 고수준 API 통합
- TPU(Tensor Processing Unit) 지원
- TPU는 GPU보다 전력을 적게 소모, 경제적
- 일반적으로 32비트(float32)로 수행되는 곱셈 연산을 16비트(float16)로 낮춤
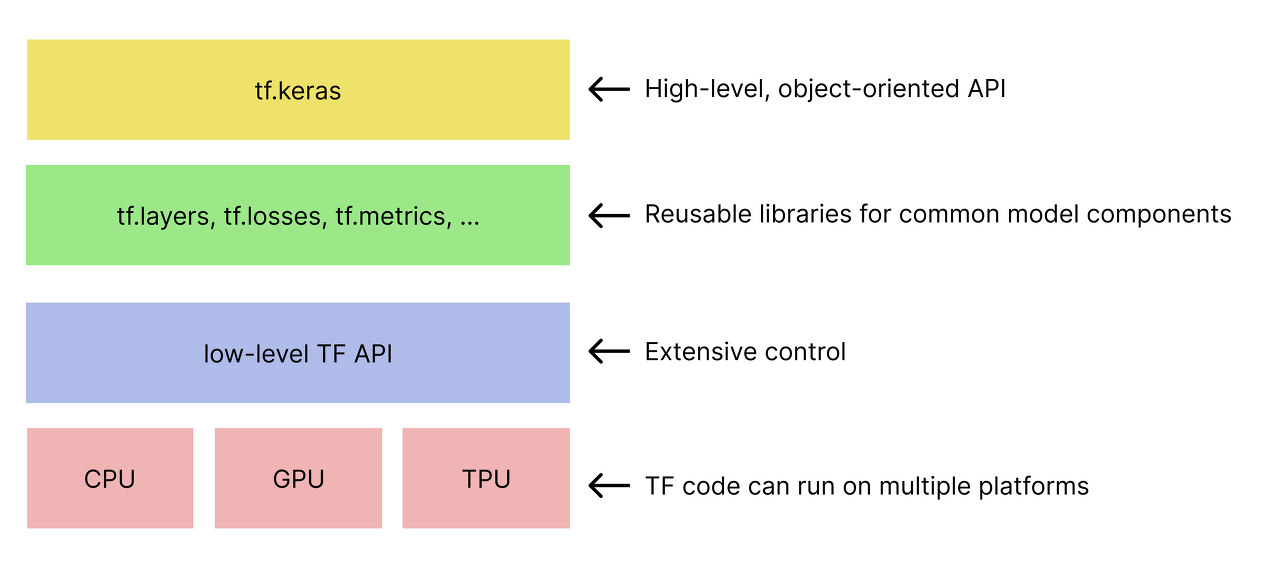
1. 텐서플로우 아키텍쳐
2. 텐서플로우 시작하기
- 텐서플로우 라이브러리
import numpy as np
import tensorflow as tf
print(tf.__version__)
# 출력 결과
2.11.0
- 텐서의 객체
- 타입(Type): string, float32, float16, int32, int8 등
- 형상(Shape): 0, 1, 2차원 등의 데이터 차원
- 축(Rank): 차원의 개수
- 텐서의 차원과 연산
a = tf.constant(2)
print(tf.rank(a))
print(a)
# 출력 결과
tf.Tensor(0, shape=(), dtype=int32)
tf.Tensor(2, shape=(), dtype=int32)- rank는 0으로 나와 차원이 0차원임을 의미
- a값은 2
- default 타입은 int32
b = tf.constant([2, 3])
print(tf.rank(b))
print(b)
# 출력 결과
tf.Tensor(1, shape=(), dtype=int32)
tf.Tensor([2 3], shape=(2,), dtype=int32)- rank는 1로 나와 차원이 1차원임을 의미
- b값은 [2, 3]
c = tf.constant([[2, 3], [6, 7]])
print(tf.rank(c))
print(c)
# 출력 결과
tf.Tensor(2, shape=(), dtype=int32)
tf.Tensor(
[[2 3]
[6 7]], shape=(2, 2), dtype=int32)- rank는 2로 나와 차원이 2차원임을 의미
- c값은
[[2, 3]
[6, 7]]
d = tf.constant(['Hello'])
print(tf.rank(d))
print(d)
# 출력 결과
tf.Tensor(1, shape=(), dtype=int32)
tf.Tensor([b'Hello'], shape=(1,), dtype=string)- rank는 1로 나와 차원이 1차원임을 의미
- d값은 'Hello'
- 타입은 string
- 난수 생성
rand = tf.random.uniform([1], 0, 1)
print(rand.shape)
print(rand)
# 출력 결과
(1,)
tf.Tensor([0.21540296], shape=(1,), dtype=float32)- random의 분포는 uniform(균등) 분포
- shape은 [1]
- 값의 최소값은 0, 최대값은 1(0에서 1 사이의 숫자 중 랜덤 추출)
rand2 = tf.random.normal([1, 2], 0, 1)
print(rand2.shape)
print(rand2)
# 출력 결과
(1, 2)
tf.Tensor([[ 0.801973 -0.2971729]], shape=(1, 2), dtype=float32)- random의 분포는 normal(정규) 분포
- shape은 [1, 2]
- 값의 분포의 평균은 0, 표준편차는 1
rand3 = tf.random.normal(shape = (3, 2), mean = 0, stddev = 1)
print(rand3.shape)
print(rand3)
# 출력 결과
(3, 2)
tf.Tensor(
[[-0.4018749 0.1871953 ]
[-0.5250586 0.95744073]
[ 2.2473423 -0.62274617]], shape=(3, 2), dtype=float32)- 정규분포에서 랜덤 값 추출하는 함수의 인수를 직접 지정하는 방법
- 즉시 실행 모드(Eager Mode) 지원
- 즉시 실행 모드를 통해 텐서플로우를 파이썬처럼 사용할 수 있음
- 1.x버전에서는 '그래프'를 생성하고, 초기화 한 뒤에 세션을 통해 값을 흐르게 하는 작업을 진행해야함
a = tf.constant(2)
b = tf.constant(3)
print(tf.add(a, b))
print(a + b)
# 출력 결과
tf.Tensor(5, shape=(), dtype=int32)
tf.Tensor(5, shape=(), dtype=int32)
print(tf.subtract(a, b))
print(a - b)
# 출력 결과
tf.Tensor(-1, shape=(), dtype=int32)
tf.Tensor(-1, shape=(), dtype=int32)
print(tf.multiply(a, b))
print(a * b)
# 출력 결과
tf.Tensor(6, shape=(), dtype=int32)
tf.Tensor(6, shape=(), dtype=int32)- add()와 +, subtract()와 -, multiply()와 *는 같은 기능
- 텐서플로우 ↔ 넘파이
- .numpy 사용 시 텐서플로우 데이터를 넘파이 형식으로 변환
c = tf.add(a, b).numpy()
print(type(c))
# 출력 결과
<class 'numpy.int32'>- tf.convert_to_tensor()를 사용해 넘파이 데이터를 텐서플로우 형식으로 변환
c_square = np.square(c, dtype = np.float32)
c_tensor = tf.convert_to_tensor(c_square)
print(c_tensor)
print(type(c_tensor))
# 출력 결과
tf.Tensor(25.0, shape=(), dtype=float32)
<class 'tensorflow.python.framework.ops.EagerTensor'>
- 넘파이처럼 사용하기
t = tf.constant([[1., 2., 3.], [4., 5., 6.]])
print(t.shape)
print(t.dtype)
# 출력 결과
(2, 3)
<dtype: 'float32'># 슬라이싱
print(t[:, 1:])
# 출력 결과
tf.Tensor(
[[2. 3.]
[5. 6.]], shape=(2, 2), dtype=float32)
# 각 행에서 인데스가 1인 값(2., 5.)만 추출
t[..., 1, tf.newaxis]
# 출력 결과
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[2.],
[5.]], dtype=float32)># 연산
# 각 원소값에 10씩 더하기
t + 10
# 출력 결과
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[11., 12., 13.],
[14., 15., 16.]], dtype=float32)>
# 각 원소값의 제곱값 출력
tf.square(t)
# 출력 결과
<tf.Tensor: shape=(2, 3), dtype=float32, numpy=
array([[ 1., 4., 9.],
[16., 25., 36.]], dtype=float32)># tensor 곱
# 원래 t 행렬(2*3) * 전치된 행렬(3*2) = 2*2 행렬
t @ tf.transpose(t)
# 출력 결과
<tf.Tensor: shape=(2, 2), dtype=float32, numpy=
array([[14., 32.],
[32., 77.]], dtype=float32)>
- 타입 변환
- 데이터 타입이 다르면 연산 불가능

- 텐서의 기본 dtype
- float형 텐서: float32
- int형 텐서: int32
- 연산 시 텐서의 타입을 맞춰줘야 함
- float32 ~ float32
- int32 ~ int32
- float32 ~ int32 (x)
- 타입 변환에는 tf.cast() 사용
# float64 타입의 데이터
t = tf.constant(30., dtype = tf.float64)
# float32 타입의 데이터(default)
t2 = tf.constant(4.)
# 잘못된 예시
# float63와 float32로 각각 타입이 다르므로 연산 불가능
print(t + t2)
# 출력 결과
InvalidArgumentError: cannot compute AddV2 as input #1(zero-based) was expected to be a double tensor but is a float tensor [Op:AddV2]
# float64 타입의 데이터를 float32 형식으로 변환
print(t2 + tf.cast(t, tf.float32))
# 출력 결과
tf.Tensor(34.0, shape=(), dtype=float32)
- AutoGraph(오토그래프)
- Tensorflow가 작업을 좀 더 빠르게 동작하게 하기 위한 방법으로 Graph로 만들어 연산을 진행
- tf.Graph
- 유연성이 있음
- 모바일 애플리케이션, 임베디드 기기, 백엔드 서버와 같이 Python 인터프리터가 없는 환경에서 Tensorflow 사용 가능
코드
- @tf.function
- 자동으로 그래프를 생성(Auto Graph)
- 그래프로 변환하여 사용 -> GPU 연산 가능
- 파이썬으로 구성된 함수를 텐서플로우의 그래프 형태로 다루고 싶을 때 사용가능
- 원본 함수가 필요하다면 (tf.function).python_function()
@tf.function
def my_function(x):
return x**2 - 10 * x + 3
print(my_function(2))
print(my_function(tf.constant(2)))
# 출력 결과
tf.Tensor(-13, shape=(), dtype=int32)
tf.Tensor(-13, shape=(), dtype=int32)# tf.function으로 지정하지 않았을 경우
def my_function_(x):
return x**2 - 10 * x + 3
print(my_function_(2))
print(my_function_(tf.constant(2)))
# 출력 결과
# 일반적인 값을 넣으면 일반적인 값으로
# tf.constant값을 넣으면 tensor값으로 출력
-13
tf.Tensor(-13, shape=(), dtype=int32)# 일반 함수를 tensor함수로 변환하기
tf_my_func = tf.function(my_function_)
print(tf_my_func(2))
print(tf_my_func(tf.constant(2)))
# 출력 결과
tf.Tensor(-13, shape=(), dtype=int32)
tf.Tensor(-13, shape=(), dtype=int32)
# tensor 함수를 일반 함수로 변환하기
tf_my_func.python_function(2)
# 출력 결과
-13def function_to_get_faster(x, y, b):
# 행렬곱
x = tf.matmul(x, y)
x = x + b
return x
a_function_that_uses_a_graph = tf.function(function_to_get_faster)
x1 = tf.constant([[1., 2.]])
y1 = tf.constant([[2.], [3.]])
b1 = tf.constant(4.)
a_function_that_uses_a_graph(x1, y1, b1).numpy()
# 출력 결과
array([[12.]], dtype=float32)# 파이썬 함수
def inner_function(x, y, b):
x = tf.matmul(x, y)
x = x + b
return x
# tensor 함수
@tf.function
def outer_function(x):
y = tf.constant([[2.], [3.]])
b = tf.constant(4.)
return inner_function(x, y, b)
# 파이썬 함수와 tensor 함수의 혼합
outer_function(tf.constant([[1., 2.]])).numpy()- 텐서플로우가 tf.function으로 변환한 코드
print(tf.autograph.to_code(my_function.python_function))
print(tf.autograph.to_code(tf_my_func.python_function))
print(tf.autograph.to_code(outer_function.python_function))
# 출력 결과
def tf__my_function(x):
with ag__.FunctionScope('my_function', 'fscope', ag__.ConversionOptions(recursive=True, user_requested=True, optional_features=(), internal_convert_user_code=True)) as fscope:
do_return = False
retval_ = ag__.UndefinedReturnValue()
try:
do_return = True
retval_ = ag__.ld(x) ** 2 - 10 * ag__.ld(x) + 3
except:
do_return = False
raise
return fscope.ret(retval_, do_return)
def tf__my_function_(x):
with ag__.FunctionScope('my_function_', 'fscope', ag__.ConversionOptions(recursive=True, user_requested=True, optional_features=(), internal_convert_user_code=True)) as fscope:
do_return = False
retval_ = ag__.UndefinedReturnValue()
try:
do_return = True
retval_ = ag__.ld(x) ** 2 - 10 * ag__.ld(x) + 3
except:
do_return = False
raise
return fscope.ret(retval_, do_return)
def tf__outer_function(x):
with ag__.FunctionScope('outer_function', 'fscope', ag__.ConversionOptions(recursive=True, user_requested=True, optional_features=(), internal_convert_user_code=True)) as fscope:
do_return = False
retval_ = ag__.UndefinedReturnValue()
y = ag__.converted_call(ag__.ld(tf).constant, ([[2.0], [3.0]],), None, fscope)
b = ag__.converted_call(ag__.ld(tf).constant, (4.0,), None, fscope)
try:
do_return = True
retval_ = ag__.converted_call(ag__.ld(inner_function), (ag__.ld(x), ag__.ld(y), ag__.ld(b)), None, fscope)
except:
do_return = False
raise
return fscope.ret(retval_, do_return)- 속도 향상
import timeit
class SequentialModel(tf.keras.Model):
def __init__(self, **kwargs):
super(SequentialModel, self).__init__(**kwargs)
self.flatten = tf.keras.layers.Flatten(input_shape = (28, 28))
self.dense_1 = tf.keras.layers.Dense(128, activation = 'relu')
self.dropout = tf.keras.layers.Dropout(0.2)
self.dense_2 = tf.keras.layers.Dense(10)
def call(self, x):
x = self.flatten(x)
x = self.dense_1(x)
x = self.dropout(x)
x = self.dense_2(x)
return x
input_data = tf.random.uniform([60, 28, 28])
eager_model = SequentialModel()
graph_model = tf.function(eager_model)
print("Eager time:", timeit.timeit(lambda: eager_model(input_data), number = 10000))
print("Graph time:", timeit.timeit(lambda: graph_model(input_data), number = 10000))
# 출력 결과
Eager time: 70.29523700000004
Graph time: 35.47442840000008- 시간 효율성에서 즉시 실행 모드(eager mode)보다 그래프 모드(graph mode)가 더 빠름
- 변수 생성
- tf.Variable
- 딥러닝 모델 학습 시, 그래프 연산이 필요할 때 사용
X = tf.Variable(20.)
print(X)
# 출력 결과
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=20.0>
- AutoGrad(자동 미분)
- tf.GradientTape API 사용
- tf.Variable 같은 일부 입력에 대한 기울기 계산
- 기본적으로 한번만 사용됨
- 변수가 포함된 연산만 기록
x = tf.Variable(3.)
with tf.GradientTape() as tape:
y = x**2
dy_dx = tape.gradient(y, x)
dy_dx.numpy()
# 출력 결과
6.0
# 한번만 연산할 수 있으므로 다른 값으로 바꿔 돌리면 오류 발생
x2 = tf.Variable(4)
dy_dx = tape.gradient(y, x2)
dy_dx.numpy()
# 출력 결과
A non-persistent GradientTape can only be used to compute one set of gradients (or jacobians)x = tf.Variable(2.)
y = tf.Variable(3.)
with tf.GradientTape() as tape:
y_sq = y**2
z = x**2 + tf.stop_gradient(y_sq)
grad = tape.gradient(z, {'x': x, 'y': y})
# x에 대한 미분
print('dz/dx:', grad['x'])
# y에 대한 미분
print('dz/dy:', grad['y'])
# 출력 결과
dz/dx: tf.Tensor(4.0, shape=(), dtype=float32)
dz/dy: None
- tf.GradientTape를 지속가능하게 사용하고 싶을 때
weights = tf.Variable(tf.random.normal((3, 2)), name = 'weights')
biases = tf.Variable(tf.zeros(2, dtype = tf.float32), name = 'biases')
x = [[1., 2., 3.]]
# 값을 영구적으로 상용할 수 있도록 persistent 옵션 주기
with tf.GradientTape(persistent = True) as tape:
y = x @ weights + biases
loss = tf.reduce_mean(y**2)
[dl_dw, dl_db] = tape.gradient(loss, [weights, biases])
print(weights.shape)
print(dl_dw.shape)
# 출력 결과
(3, 2)
(3, 2)
3. 간단한 신경망 구조
- 뉴런
- 입력 → 연산 → 활성화 함수 → 출력
def sigmoid(x):
return (1 / (1 + np.exp(-x)))
def Neuron(x, W, bias = 0):
z = x * W + bias
return sigmoid(z)
# tensor데이터 입력(형태에 맞게 random값을 연습용으로 생성)
x = tf.random.normal((1, 2), 0, 1)
W = tf.random.normal((1, 2), 0, 1)
print('x.shape:', x.shape)
print('W.shape:', W.shape)
print(x)
print(W)
print(Neuron(x, W))
# 출력 결과
x.shape: (1, 2)
W.shape: (1, 2)
tf.Tensor([[0.7348223 0.89396125]], shape=(1, 2), dtype=float32)
tf.Tensor([[ 0.69655097 -0.5962996 ]], shape=(1, 2), dtype=float32)
[[0.625238 0.36980146]]
- 퍼셉트론 학습 알고리즘(가중치 업데이트)
$$ w^{(nextstep)}=w+\eta(y-\widetilde{y})x $$
- \(w\): 가중치
- \(\eta\): 학습률
- \(y\): 정답 레이블
- \(\widetilde{y}\): 예측 레이블
# 한 번의 뉴런을 거쳤을 때
x = 1
y = 0
W = tf.random.normal([1], 0, 1)
print(Neuron(x, W))
print('y:', y)
# 출력 결과
[0.8723855]
y: 0# 1000번 반복
for i in range(1000):
output = Neuron(x, W)
error = y - output
# learning rate 0.1
W = W + x * 0.1 * error
if i % 100 == 99:
print('{}\t{}\t{}'.format(i+1, error, output))
# 출력 결과
100 [-0.13575228] [0.13575228]
200 [-0.06054739] [0.06054739]
300 [-0.03837379] [0.03837379]
400 [-0.02797328] [0.02797328]
500 [-0.02197183] [0.02197183]
600 [-0.01807551] [0.01807551]
700 [-0.01534558] [0.01534558]
800 [-0.01332812] [0.01332812]
900 [-0.01177713] [0.01177713]
1000 [-0.01054805] [0.01054805]# 다른 뉴런 정의
def Neuron2(x, W, bias = 0):
z = tf.matmul(x, W, transpose_b = True) + bias
return sigmoid(z)
x = tf.random.normal((1, 3), 0, 1)
y = tf.ones(1)
W = tf.random.normal((1, 3), 0, 1)
print(Neuron2(x, W))
print('y:', y)
# 출력 결과
[[0.03847362]]
y: tf.Tensor([1.], shape=(1,), dtype=float32)
# 1000번 반복
for i in range(1000):
output = Neuron2(x, W)
error = y - output
W = W + x * 0.1 * error
if i % 100 == 99:
print('{}\t{}\t{}'.format(i+1, error, output))
# 출력 결과
100 [[0.0317629]] [[0.9682371]]
200 [[0.01478064]] [[0.98521936]]
300 [[0.00960499]] [[0.990395]]
400 [[0.00710833]] [[0.99289167]]
500 [[0.00564009]] [[0.9943599]]
600 [[0.00467372]] [[0.9953263]]
700 [[0.0039897]] [[0.9960103]]
800 [[0.00348008]] [[0.9965199]]
900 [[0.00308585]] [[0.99691415]]
1000 [[0.00277168]] [[0.9972283]]# 가중치 추가
x = tf.random.normal((1, 3), 0, 1)
weights = tf.random.normal((1, 3), 0, 1)
bias = tf.zeros((1, 1))
y = tf.ones((1, ))
print("x\t: {}\nweights\t: {}\nbias\t: {}".format(x, weights, bias))
# 출력 결과
x : [[ 1.2705061 1.3811893 -0.14885783]]
weights : [[-1.1372662 -0.28991228 -1.5178484 ]]
bias : [[0.]]
# 1000번 반복
for i in range(1000):
output = Neuron2(x, weights, bias = bias)
error = y - output
weights = weights + x * 0.1 * error
bias = bias + 1 * 0.1 * error
if i % 100 == 99:
print('{}\t{}\t{}'.format(i+1, error, output))
# 출력 결과
100 [[0.02399486]] [[0.97600514]]
200 [[0.01155555]] [[0.98844445]]
300 [[0.00759584]] [[0.99240416]]
400 [[0.00565416]] [[0.99434584]]
500 [[0.00450194]] [[0.99549806]]
600 [[0.00373942]] [[0.9962606]]
700 [[0.00319755]] [[0.99680245]]
800 [[0.00279278]] [[0.9972072]]
900 [[0.00247878]] [[0.9975212]]
1000 [[0.00222832]] [[0.9977717]]
# 초기값과 바뀐 weights값과 bias 값
print("x\t: {}\nweights\t: {}\nbias\t: {}".format(x, weights, bias))
# 출력 결과
x : [[ 1.2705061 1.3811893 -0.14885783]]
weights : [[ 1.0225528 2.058065 -1.7709007]]
bias : [[1.6999679]]- AND 게이트
X = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
Y = np.array([[1], [0], [0], [0]])
W = tf.random.normal([2], 0, 1)
b = tf.random.normal([1], 0, 1)
b_x = 1
for i in range(2000):
error_sum = 0
for j in range(4):
output = sigmoid(np.sum(X[j] * W) + b_x + b)
error = Y[j][0] - output
W = W + X[j] * 0.1 * error
b = b + b_x * 0.1 * error
error_sum += error
if i % 200 == 0:
print("Epoch {:4d}\tError Sum: {}".format(i, error_sum))
print('\n가중치\t:{}'.format(W))
print("편향\t: {}".format(b))
# 출력 결과
Epoch 0 Error Sum: [-2.8165922]
Epoch 200 Error Sum: [-0.11301513]
Epoch 400 Error Sum: [-0.06664746]
Epoch 600 Error Sum: [-0.04715659]
Epoch 800 Error Sum: [-0.03637875]
Epoch 1000 Error Sum: [-0.02955558]
Epoch 1200 Error Sum: [-0.02485914]
Epoch 1400 Error Sum: [-0.02143379]
Epoch 1600 Error Sum: [-0.01882876]
Epoch 1800 Error Sum: [-0.01678012]
가중치 :[6.9653535 6.968502 ]
편향 : [-11.627143]# 평가
for i in range(4):
print("X: {} Y: {} Output: {}".format(X[i], Y[i], sigmoid(np.sum(X[i] * W) + b)))
# 출력 결과
# 정답인 [1, 1]에 대해서만 0.9이상의 높은 output을 가짐
X: [1 1] Y: [1] Output: [0.9094314]
X: [1 0] Y: [0] Output: [0.00936108]
X: [0 1] Y: [0] Output: [0.00939032]
X: [0 0] Y: [0] Output: [8.92056e-06]
- OR 게이트
X2 = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
Y2 = np.array([[1], [1], [1], [0]])
W2 = tf.random.normal([2], 0, 1)
b2 = tf.random.normal([1], 0, 1)
b_x = 1
for i in range(2000):
error_sum = 0
for j in range(4):
output = sigmoid(np.sum(X2[j] * W2) + b_x + b2)
error = Y2[j][0] - output
W2 = W2 + X2[j] * 0.1 * error
b2 = b2 + b_x * 0.1 * error
error_sum += error
if i % 200 == 0:
print("Epoch {:4d}\tError Sum: {}".format(i, error_sum))
print('\n가중치\t:{}'.format(W2))
print("편향\t: {}".format(b2))
# 출력 결과
Epoch 0 Error Sum: [0.5757617]
Epoch 200 Error Sum: [-0.05437072]
Epoch 400 Error Sum: [-0.02711956]
Epoch 600 Error Sum: [-0.0179592]
Epoch 800 Error Sum: [-0.01337508]
Epoch 1000 Error Sum: [-0.01063495]
Epoch 1200 Error Sum: [-0.0088167]
Epoch 1400 Error Sum: [-0.00752456]
Epoch 1600 Error Sum: [-0.00655934]
Epoch 1800 Error Sum: [-0.00581255]
가중치 :[8.188078 8.187768]
편향 : [-4.628335]# 평가
for i in range(4):
print("X: {} Y: {} Output: {}".format(X2[i], Y2[i], sigmoid(np.sum(X2[i] * W2) + b2)))
# 출력 결과
# 정답인 [1, 1], [1, 0], [0, 1]에 대해서 0.97 이상의 높은 output 가짐
X: [1 1] Y: [1] Output: [0.99999213]
X: [1 0] Y: [1] Output: [0.9723406]
X: [0 1] Y: [1] Output: [0.97233236]
X: [0 0] Y: [0] Output: [0.00967647]
- XOR 게이트
X3 = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
Y3 = np.array([[0], [1], [1], [0]])
W3 = tf.random.normal([2], 0, 1)
b3 = tf.random.normal([1], 0, 1)
b_x = 1
for i in range(2000):
error_sum = 0
for j in range(4):
output = sigmoid(np.sum(X3[j] * W3) + b_x + b3)
error = Y3[j][0] - output
W3 = W3 + X3[j] * 0.1 * error
b3 = b3 + b_x * 0.1 * error
error_sum += error
if i % 200 == 0:
print("Epoch {:4d}\tError Sum: {}".format(i, error_sum))
print('\n가중치\t:{}'.format(W3))
print("편향\t: {}".format(b3))
# 출력 결과
Epoch 0 Error Sum: [1.3929144]
Epoch 200 Error Sum: [0.00576425]
Epoch 400 Error Sum: [0.00023448]
Epoch 600 Error Sum: [9.596348e-06]
Epoch 800 Error Sum: [6.556511e-07]
Epoch 1000 Error Sum: [5.364418e-07]
Epoch 1200 Error Sum: [5.364418e-07]
Epoch 1400 Error Sum: [5.364418e-07]
Epoch 1600 Error Sum: [5.364418e-07]
Epoch 1800 Error Sum: [5.364418e-07]
가중치 :[5.1282957e-02 1.1660159e-06]
편향 : [-1.0000018]# 평가
for i in range(4):
print("X: {} Y: {} Output: {}".format(X3[i], Y3[i], sigmoid(np.sum(X3[i] * W3) + b3)))
# 출력 결과
# 학습이 잘 되지 않음
X: [1 1] Y: [0] Output: [0.2791428]
X: [1 0] Y: [1] Output: [0.27914253]
X: [0 1] Y: [1] Output: [0.2689413]
X: [0 0] Y: [0] Output: [0.26894107]
# 레이어 추가
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
np.random.seed(111)
X4 = np.array([[1, 1], [1, 0], [0, 1], [0, 0]])
Y4 = np.array([[0], [1], [1], [0]])
model = Sequential([Dense(units = 2, activation = 'sigmoid', input_shape = (2, )),
Dense(units = 1, activation = 'sigmoid'),])
model.compile(optimizer = tf.keras.optimizers.SGD(learning_rate = 0.1), loss = 'mse')
model.summary()
# 출력 결과
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_6 (Dense) (None, 2) 6
dense_7 (Dense) (None, 1) 3
=================================================================
Total params: 9
Trainable params: 9
Non-trainable params: 0
_________________________________________________________________history = model.fit(X4, Y4, epochs = 2000, batch_size = 1, verbose = 1)
# XOR 게이트 학습 결과
model.predict(X4)
# 출력 결과
# 실제 정답인 0, 1, 1, 0에 가깝게 나온 것을 확인
1/1 [==============================] - 0s 122ms/step
array([[0.20889895],
[0.84853107],
[0.84807545],
[0.11541054]], dtype=float32)
- XOR 게이트의 'LOSS' 시각화
plt.plot(history.history['loss'])
'Python > Deep Learning' 카테고리의 다른 글
| [딥러닝-케라스] 케라스 기초(1) (0) | 2023.04.26 |
|---|---|
| [딥러닝-텐서플로우] 텐서플로우 회귀 모델 (0) | 2023.04.26 |
| [딥러닝 기초] RNN(순환신경망) (0) | 2023.03.27 |
| [딥러닝 기초] 자연어 처리 (0) | 2023.03.27 |
| [딥러닝 기초] CNN(합성곱 신경망)(2) (0) | 2023.03.23 |