1. 정규방정식
-선형 회귀 모형에서 비용함수(RMSE 또는 MSE 등)을 최소화하는 회귀 계수 θ를 찾기 위한 해석적인 방법

-공식 검증
import numpy as np
import matplotlib.pyplot as plt
# 선형관계에 있는 변수 X, y 100개씩 100행 1열의 배열로 생성
X=2*np.random.rand(100,1)
y=4+3*X+np.random.randn(100,1)
plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()
X_b=np.c_[np.ones((100,1)),X] # 모든 샘플에 X0=1을 추가
# X0에 1을 추가한 독립변수 배열에 배열을 전치시킨 것을 곱하여
# 그 역행렬을 구하고
# 역행렬과 독립변수 배열을 전치시킨 배열을 곱한 뒤
# 종속변수 행렬 곱하기
theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best
### 결과 ###
array([[4.1140573 ],
[2.81512351]])-엑셀을 이용해 theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) 계산과정 설명
1) 이해를 위해 X와 y 변수에서 각각 세개씩만 데이터 추출한 뒤 X_b, y 배열 생성
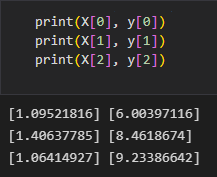
X_b=np.array([[1.09521816,1],
[1.40637785,1],
[1.06414927,1]])
y=np.array([[6.00397116],
[8.4618674],
[9.23386642]])
2) 엑셀에서 배열 생성

3) X_b.T : 전치
X_b배열을 복사하여 행/열 바꿔서 붙여넣기

4) X_b.T.dot(X_b) : 전치한 행렬과 원래 행렬 곱하기

-"=MMULT(전치행렬, 원래행렬)" 식 작성 후 Ctrl+Shift+Enter
5) np.linarg.inv(X_b.T.dot(X_b)) : 역행렬

-"=MINVERSE(행렬)" 식 작성 후 Ctrl+Shift+Enter
6) np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T) : 5)에서 구한 역행렬과 3)에서 전치시켰던 행렬 곱하기
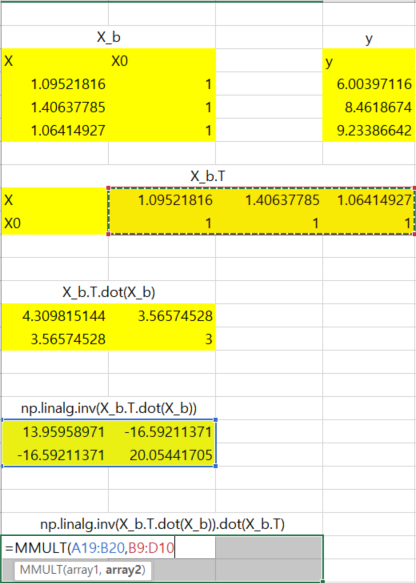
-"=MMULT(행렬, 행렬)" 식 작성 후 Ctrl+Shift+Enter
7) np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) : 마지막 y 행렬 곱하기

-"=MMULT(행렬, 행렬)" 식 작성 후 Ctrl+Shift+Enter
8) 결과

-파이썬과 비교해보면 똑같은 값이 나옴

-위와 같은 과정을 거쳐서 나온 theta_best를 이용하여 새로운 값에 대한 y값 예측하기
# 새로운 값을 예측
# 0과 2를 모델에 넣었을 때 각각의 예측값
X_new=np.array([[0],[2]])
X_new_b=np.c_[np.ones((2,1)),X_new]
y_predict=X_new_b.dot(theta_best)
y_predict
### 결과 ###
array([[4.25816196],
[9.8437471 ]])-예측한 0과 2의 값으로 예측된 회귀직선 그려보기
# 그래프로 표시
plt.plot(X_new,y_predict,'r-')
plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()
-사이킷런에서 선형회귀
# 사이킷런에서 선형 회귀 모형
from sklearn.linear_model import LinearRegression
# 선형 회귀 모형 객체 생성
lin_reg=LinearRegression()
# X와 y를 모형에 피팅
lin_reg.fit(X,y)
# 선형회귀 모형의 절편과 회귀계수
lin_reg.intercept_, lin_reg.coef_
### 결과 ###
(array([4.25816196]), array([[2.79279257]]))
# 새로운 값(0,2)에 대한 예측
lin_reg.predict(X_new)
### 결과 ###
array([[4.25816196],
[9.8437471 ]])
-LinearRegression 클래스는 scipy.linalg,lstsq() 함수를 기반으로 함
-함수를 직접 호출하면 sklearn의 LinearRegressor()에서 구했던 절편과 회귀계수와 같은 값이 출력
# scipy.linalg.lstsq() 함수
theta_best_svd,residuals,rank,s=np.linalg.lstsq(X_b,y,rcond=1e-6)
theta_best_svd
### 결과 ###
array([[4.25816196],
[2.79279257]])-scipy.linalg.lstsq() 함수는 다음 식을 계산함 $$\hat{\theta }=X^+y$$
-X+는 X의 유사역행렬
-유사역행렬은 특잇값 분해(SVD)라 부르는 표준 행렬 분해 기법을 사용해 계산
2. 계산 복잡도
-정규 방정식은 (n+1)*(n+1) 크기가 되는 $$X^TX$$의 역행렬 계산
-역행렬을 계산하는 계산 복잡도는 특성 수가 n배로 늘어나면 계산시간이 n^2.4에서 n^3 사이로 늘어남
-사이킷런의 LinearRegression 클래스가 사용하는 SVD 방법은 약 n^2로 특성 수가 두 배 늘어나면 계산시간은 대략 4배 늘어남
-정규방정식이나 다른 알고리즘으로 학습된 선형 회귀모델은 예측이 매우 빠름
(예측 계산 복잡도는 샘플 수와 특성 수에 선형적으로 샘플(또는 특성)이 두배 증가하면 걸리는 시간도 거의 두배 증가)
'Python > Machine Learning' 카테고리의 다른 글
| [머신러닝 알고리즘] 사이킷런 제대로 시작하기(2) (0) | 2022.12.28 |
|---|---|
| [머신러닝 알고리즘] 사이킷런 제대로 시작하기(1) (1) | 2022.12.26 |
| [ML] 분류 (2) - 다중 분류 (0) | 2022.10.27 |
| [ML] 분류 (1) - 이진 분류 (0) | 2022.10.26 |
| [ML] 머신러닝 프로젝트의 베이스라인 (0) | 2022.10.25 |