6. model_selection 모듈
-학습용 데이터와 테스트 데이터로 분리
-교차 검증 분할 및 평가
-Estimator의 하이퍼 파라미터 튜닝을 위한 다양한 함수와 클래스 제공
-train_test_split(): 학습/테스트 세트 분리
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
# diabetes 데이터 세트 불러오기
diabetes = load_diabetes()
# diabetes 데이터 세트를 train데이터와 test 데이터로 쪼개기
# train_test_split의 인자는 X(feature 데이터), y(target 데이터), test_size(테스트 데이터 비율)
# 4개의 값을 반환(feature 데이터 훈련용 / 테스트용, target 데이터 훈련용 / 테스트용)
X_train, x_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size = 0.3)
# 선형회귀모델 적용해보고 점수 확인하기
model = LinearRegression()
model.fit(X_train, y_train)
print("학습 데이터 점수: {}".format(model.score(X_train, y_train)))
print("평가 데이터 점수: {}".format(model.score(X_test, y_test)))
# 출력결과
학습 데이터 점수: 0.5097761792435763
평가 데이터 점수: 0.5120316690456863# 모델에 의해 예측된 X_test에 대한 y_test값(y_pred)과 원래의 y_test값 비교 시각화
import matplotlib.pyplot as plt
y_pred = model.predict(X_test)
plt.figure(figsize = (8,4))
plt.scatter(y_test, y_pred)
plt.plot([30, 350], [30, 350], '--r')
plt.tight_layout()

→ x축이 실제 정답, y축이 예측된 값
→ 빨간선에 가까울수록 잘 맞춘 것이고, 빨간선에 가까운 점이 적으므로 점수도 0.5정도밖에 나오지 않음
→ 다른 모델을 사용하던지, 전처리 과정의 조정으로 점수를 점점 개선시켜야 함
-cross_val_score(): 교차 검증

→ 교차검증은 위 그림과 같이 데이터를 여러 개로 쪼개어 한 부분을 검증용으로, 나머지 부분을 테스트용으로 사용하여 각각의 점수를 계산
from sklearn.model_selection import cross_val_score, cross_validate
import numpy as np
# 인자는 LinearRegression를 담은 model, feature 데이터 세트, target 데이터 세트
# 마지막 인자는 교차 검증을 위해 데이터를 몇 개의 세트로 분리할 것인지 지정
# 교차 검증은 분리한 데이터 세트 개수만큼 진행
scores = cross_val_score(model, diabetes.data, diabetes.target, cv = 5)
# 데이터를 5개로 나누어 각 세트에 대해 한번씩 교차검증을 진행하여 총 5번 진행하고 각각의 점수 출력
print("교차 검증 정확도: {}".format(scores))
# 모든 점수 리스트의 평균과 표준편차 출력
print("교차 검증 정확도의 평균: {} +/- {}".format(np.mean(scores), np.std(scores)))
# 출력 결과
교차 검증 정확도: [0.42955615 0.52259939 0.48268054 0.42649776 0.55024834]
교차 검증 정확도의 평균: 0.48231643590864215 +/- 0.04926857751190378
-GridSearchCV: 교차 검증을 반복하며 최적의 하이퍼 파라미터 찾기
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import Ridge
import pandas as pd
# Ridge 모델에서 최적의 점수를 도출하는 alpha값의 후보
alpha = [0.001, 0.01, 0.1, 1, 10, 100, 1000]
# gridsearch를 통해 찾을 하이퍼파라미터 값과 후보 하이퍼파라미터 값을 딕셔너리 형태로 지정
param_grid = dict(alpha = alpha)
# GridSearch를 통해 최적 하이퍼 파라미터를 모델(Ridge), 하이퍼파라미터 후보, 교차검증 횟수
gs = GridSearchCV(estimator = Ridge(), param_grid = param_grid, cv = 10)
# fit하는 과정은 일반 모델과 동일
result = gs.fit(diabetes.data, diabetes.target)
print("최적 점수: {}".format(result.best_score_))
print("최적 파라미터: {}".format(result.best_params_))
print(gs.best_estimator_)
pd.DataFrame(result.cv_results_)
# 출력 결과
최적 점수: 0.46332219117960366
최적 파라미터: {'alpha': 0.1}
Ridge(alpha=0.1)
→ result.cv_results_에 대한 출력결과로, 각 하이퍼파라미터에 대한 10번의 교차 검증의 결과가 전부 표로 정리되어 출력
-multiprocessing을 이용한 GridSearchCV
import multiprocessing
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
# 새롭게 diabetes가 아닌 iris 데이터로 연습
iris = load_iris()
# 모델도 새롭게 LinearRegression 모델을 사용하고 그에 맞는 하이퍼파라미터 후보 지정
param_grid = [{'penalty': ['l1', 'l2'],
'C': [1.5, 2.0, 2.5, 3.0, 3.5]}]
# multiprocessing을 통해 cpu 개수만큼 job을 생성해서 모델을 실행
gs = GridSearchCV(estimator = LogisticRegression(), param_grid = param_grid,
scoring = 'accuracy', cv = 10, n_jobs = multiprocessing.cpu_count())
# 이후 동일
result = gs.fit(iris.data, iris.target)
print("최적 점수: {}".format(result.best_score_))
print("최적 파라미터: {}".format(result.best_params_))
print(gs.best_estimator_)
pd.DataFrame(result.cv_results_)
# 출력 결과
최적 점수: 0.9800000000000001
최적 파라미터: {'C': 2.5, 'penalty': 'l2'}
LogisticRegression(C=2.5)
→ 모든 penalty값과 C값의 조합에서 교차 검증이 진행되므로 (C값 후보 5개 × penalty값 후보 2개 = 총 10개)의 경우에 10번씩의 교차검증 과정이 진행
7. preprocessing 모듈
-데이터 전처리 모듈
-데이터의 특징 스케일링(feature scaling): 데이터 값의 범위를 조정, 표준화와 정규화 방법이 있음
- 표준화 방법(Standaradization): \( x_{i}^{'}=\frac{x_i - mean(x)}{stdev(x)} \)
- 정규화 방법(Normalization): \( x_{i}^{'}=\frac{x_i - min(x)}{max(x) - min(x)} \)
- scikit-learn에서는 개별 벡터 크기를 맞추는 형태로 정규화하므로 minmax를 사용한 방법과 차이는 있지만 결국 같은 방법이긴함
-StandardScaler: 표준화 클래스
iris = load_iris()
iris_df = pd.DataFrame(data = iris.data, columns = iris.feature_names)
iris_df.describe()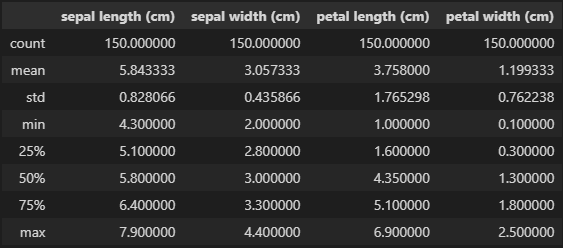
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# fit을 통해 표준화에 필요한 정보를 가져오고, transform을 통해 표준화 동작 실행
# fit_transform의 return값은 넘파이 배열
iris_scaled = scaler.fit_transform(iris_df)
iris_df_scaled = pd.DataFrame(data = iris_scaled, columns = iris.feature_names)
iris_df_scaled.describe()
→ StandardScaler를 실행하기 전과 비교하면 평균은 0에 가까운 값으로, 표준편차는 1에 가까운 값으로 표준화됨
import multiprocessing
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
X_train, X_test, y_train, y_test = train_test_split(iris_df_scaled, iris.target, test_size = 0.3)
model = LogisticRegression()
model.fit(X_train, y_train)
print("훈련 데이터 점수: {}".format(model.score(X_train, y_train)))
print("평가 데이터 점수: {}".format(model.score(X_test, y_test)))
# 출력 결과
훈련 데이터 점수: 0.9904761904761905
평가 데이터 점수: 0.9111111111111111→ 표준화된 데이터에 대해 모델에 적용시키면 평가 데이터 점수에서도 높은 점수를 받을 수 있음
-MinMaxScaler: 정규화 클래스
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
iris_scaled = scaler.fit_transform(iris_df)
iris_df_scaled = pd.DataFrame(data = iris_scaled, columns = iris.feature_names)
iris_df_scaled.describe()
→ MinMaxScaler를 실행하기 전과 비교해서 최소값은 0, 최대값은 1에 맞춰 정규화됨
X_train, X_test, y_train, y_test = train_test_split(iris_df_scaled, iris.target, test_size = 0.3)
model = LogisticRegression()
model.fit(X_train, y_train)
print("훈련 데이터 점수: {}".format(model.score(X_train, y_train)))
print("평가 데이터 점수: {}".format(model.score(X_test, y_test)))
# 출력 결과
훈련 데이터 점수: 0.9333333333333333
평가 데이터 점수: 0.9111111111111111→ 정규화된 데이터에 대해서도 모델에 적용시키면 높은 점수를 받을 수 있음
8. 성능 평가 지표
-정확도(Accuracy)
- 정확도는 전체 예측 데이터 건수 중(실제 데이터와 비교하여) 예측 결과가 동일한 데이터 건수로 계산
- scikit-learn에서는 accuracy_score 함수 제공
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# n_samples: 샘플 개수
# n_features: feature 데이터 개수
# n_informative: 의미있는 변수 개수
# n_redundant: 노이즈
# n_cluster_per_class: 클래스 당 군집 개수
X, y = make_classification(n_samples = 1000, n_features = 2, n_informative = 2, n_redundant = 0, n_clusters_per_class = 1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
model = LogisticRegression()
model.fit(X_train, y_train)
print("훈련 데이터 점수: {}".format(model.score(X_train, y_train)))
print("평가 데이터 점수: {}".format(model.score(X_test, y_test)))
predict = model.predict(X_test)
print('정확도: {}'.format(accuracy_score(y_test, predict)))
# 출력 결과
훈련 데이터 점수: 0.9114285714285715
평가 데이터 점수: 0.9266666666666666
정확도: 0.9266666666666666→ 정확도는 항상 평가 데이터 점수와 같게 나옴
- 오차 행렬(Confusion Matrix)
- True Negative(TN): 예측값을 Negative로 예측, 실제 값도 Negative
- False Positive(FP): 예측값을 Positive로 예측, 실제 값은 Negative
- False Negative(FN): 예측값을 Negative로 예측, 실제 값은 Positive
- True Positive(TP): 예측값을 Positive로 예측, 실제 값도 Positive
from sklearn.metrics import confusion_matrix
# 실제값에 y_test를, 예측값에 X_test를 model에 넣어 예측한 predict를 넣고 오차 행렬 출력
confmat = confusion_matrix(y_true = y_test, y_pred = predict)
print(confmat)
# 출력 결과
[[137 11]
[ 11 141]]# 오차 행렬 시각화
fig, ax = plt.subplots(figsize = (2.5, 2.5))
# matshow()로 히트맵 그리기
# cmap(color map)은 Blue로 설정, alpha(투명도)는 0.3
ax.matshow(confmat, cmap = plt.cm.Blues, alpha = 0.3)
# 오차 행렬(confmap)의 행(shape[0]), 열(shape[1]) 개수만큼씩 반복하여
# 행렬의 각 칸마다 text 삽입(1행 1열에 오차 행렬의 1행 1열의 값을 문자로 삽입...)
# 수직(vertical alignment), 수평(horizontal alignment) 정렬은 모두 center로 설정
for i in range(confmat.shape[0]):
for j in range(confmat.shape[1]):
ax.text(x = j , y = i, s = confmat[i, j], va = 'center', ha = 'center')
# X축 label은 Predicted label(예측한 값이 무엇인지 나타냄)
# Y축 label은 True label(실제 값이 무엇인지 나타냄)
# tight_layout()을 사용하여 figure와 subplot간 여백을 기본값으로 설정
plt.xlabel('Predicted label')
plt.ylabel('True label')
plt.tight_layout()
plt.show()
→ 1사분면: 1로 예측, 실제 0 (FP)
→ 2사분면: 0로 예측, 실제 0 (TN)
→ 3사분면: 0로 예측, 실제 1 (FN)
→ 4사분면: 1로 예측, 실제 1 (TP)
-정밀도와 재현율
- 정밀도 = TP / (FP + TP), Negative인 것을 Positive로 잘못 판단할 때 큰 문제가 있는 경우 중요
- 재현율 = TP / (FN + TP), Positive인 것을 Negative로 잘못 판단할 때 큰 문제가 있는 경우 중요
- 정확도 = (TN + TP) / (TN + FP + FN + TP)
- 오류율 = (FN + FP) / (TN + FP + FN + TP)
from sklearn.metrics import precision_score, recall_score
# 정밀도
precision = precision_score(y_test, predict)
# 재현율
recall = recall_score(y_test, predict)
print("정밀도: {}".format(precision))
print("재현율: {}".format(recall))
# 출력 결과
정밀도: 0.9276315789473685
재현율: 0.9276315789473685
- F1 Score
- 정밀도와 재현율을 결합한 지표
- 정밀도와 재현율이 어느 한쪽으로 치우치지 않을 때 높은 값(재현율과 정밀도는 trade off 관계이며, 둘 다 어느정도 높은 값을 가지도록 하고 싶을 때, F1 Score 사용)
$$ F1=2 \times \frac { precision \times recall} { precision + recall } $$
from sklearn.metrics import f1_score
# f1 score
f1 = f1_score(y_test, predict)
print("F1 score: {}".format(f1))
# 출력 결과
F1 score: 0.9276315789473685
- ROC 곡선과 AUC
- ROC 곡선은 FPR(False Positive Rate)이 변할 때, TPR(True Positive Rate)이 어떻게 변하는지 나타내는 곡선
- TPR: TP / (FN + TP), 재현율, 민감도(Sensitivity), 실제값이 양성인 것이 정확히 예측되어야 하는 수준
- TNR: TN / (FP + TN), 특이도, 실제값이 음성인 것이 정확히 예측되어야 하는 수준
- FPR: FP / (FP + TN), 1 - TNR
→ FPR을 0부터 1까지 변화시키며 TPR의 변화를 그린 곡선
→ 임계값(threshold)의 활용: 분류 결정 임계값은 양성 예측값을 결정하는 확률의 기준
→ 임계값을 1로 지정하면 양성 예측 기준이 1이 되어, 양성일 확률이 1보다 커야 양성으로 예측하는데, 1보다 클 수 없으므로 무조건 음성으로 예측함, 이때, FPR 공식에서 분자 FP는 0이 되므로 FPR은 0이 됨
→ 반대로, 임계값을 0으로 지정하면, 무조건 양성으로 예측하여 TN이 0이 되고 FPR = FP / FP = 1이 됨
→ 위의 방법으로 FPR을 0부터 1까지 변화시키며 TPR 값의 변화를 관찰
from sklearn.metrics import roc_curve
# model에 X_test값을 넣었을 때, 각 값에 대해 양성으로 예측할 확률
pred_proba_class1 = model.predict_proba(X_test)[:, 1]
# roc_curve의 인자는 실제값(y_test), 양성 예측확률(predict_proba의 두번째 열)
fprs, tprs, thresholds = roc_curve(y_test, pred_proba_class1)
# FPR과 TPR 간의 그래프(ROC 곡선)
plt.plot(fprs, tprs, label = 'ROC')
# (0, 0)에서 (1, 1)을 잇는 직선으로, 완전 랜덤한 추측이 이루어졌을 때(가장 안좋은 상황일 때)를 나타냄
plt.plot([0, 1], [0, 1], '--k', label = 'Random')
# xlim()이 0부터 1이므로, start와 end는 각각 0, 1
start, end = plt.xlim()
# x축값은 0, 1에서부터 0.1씩 커지며 소수점 두번째까지 반올림
plt.xticks(np.round(np.arange(start, end, 0.1), 2))
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.xlabel('FPR(1-TNR)')
plt.ylabel('TPR(Recall)')
plt.legend()→ 각 임계값에 대해 그 임계값 이상의 양성예측 확률을 가진 것만 양성으로 예측했을 때의 오차행렬을 계산
→ 그 오차행렬로부터 FPR(FP / (FP + TN)), TPR(TP / (FN + TP))을 계산
# model.predict_proba(X_test)의 출력값
# 0열은 음성일 확률, 1열은 양성일 확률
# 1열의 양성일 확률과 임계값을 비교하여 임계값 이상의 것만 양성으로 판단
# 이렇게 판단한 값과 실제값(y_test)를 비교하여 오차행렬을 만들면 그에 따른 FPR, TPR 계산 가능
array([[1.01487800e-02, 9.89851220e-01],
[4.37551716e-02, 9.56244828e-01],
[9.97233002e-01, 2.76699767e-03],
[5.02728650e-03, 9.94972714e-01],
[1.39106181e-02, 9.86089382e-01],
[9.85028531e-01, 1.49714687e-02],
[2.63580374e-02, 9.73641963e-01],
[9.94944361e-01, 5.05563867e-03],
[9.72061703e-03, 9.90279383e-01],
[2.28855348e-03, 9.97711447e-01],
[9.99983728e-01, 1.62719028e-05],
[9.92155567e-01, 7.84443295e-03],
[2.27501886e-02, 9.77249811e-01],
[9.98637794e-01, 1.36220602e-03],
[2.54748755e-02, 9.74525124e-01],
[9.93339766e-01, 6.66023394e-03],
[3.90060776e-02, 9.60993922e-01],
[7.02834321e-01, 2.97165679e-01],
[9.99899997e-01, 1.00002794e-04],
[3.66162097e-03, 9.96338379e-01],
[9.94623675e-01, 5.37632451e-03],
[2.93344676e-03, 9.97066553e-01],
[2.68465302e-02, 9.73153470e-01],
[1.49182896e-05, 9.99985082e-01],
[3.45351748e-02, 9.65464825e-01],
...
[3.20673218e-02, 9.67932678e-01],
[9.94737158e-01, 5.26284187e-03],
[7.22599615e-01, 2.77400385e-01],
[3.29609357e-03, 9.96703906e-01],
[1.18750772e-01, 8.81249228e-01]])→ 완전 랜덤이라면: 임계값이 몇이든 반은 맞고 반은 틀림
→ 잘 예측했다면: 양성으로 예측 확률이 0.5이상인 것에 대해 전부 양성이고 실제도 양성이라면, 임계값이 0.5가 될 때까지 양성을 잘 맞춘 비율인 TPR이 급격히 증가할 것이고, 그 이후에는 0.5미만인 것도 양성으로 예측하여 실제 음성인 것을 양성으로 예측한 비율인 FPR이 증가하기만 하여 아래와 같은 그래프가 나옴
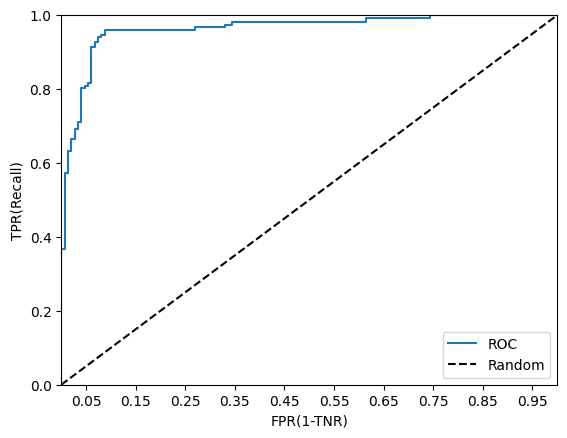
→ 점선에 가까울수록 성능이 안좋음
- AUC(Area Under Curve): ROC 곡선 밑의 면적(1에 가까울수록 좋은 값이며, 최소 0.5는 랜덤한 데이터라고 보면 됨)
from sklearn.metrics import roc_auc_score
# AUC 점수 간단하게 계산하기
roc_auc = roc_auc_score(y_test, predict)
print("ROC_AUC_Score: {}".format(roc_auc))
# 출력 결과
ROC_AUC_Score: 0.926653627311522'Python > Machine Learning' 카테고리의 다른 글
| [머신러닝 알고리즘] 선형 회귀(2) (0) | 2023.01.02 |
|---|---|
| [머신러닝 알고리즘] 선형 회귀(1) (0) | 2022.12.29 |
| [머신러닝 알고리즘] 사이킷런 제대로 시작하기(1) (1) | 2022.12.26 |
| [ML] 모델 훈련 (1) - 선형회귀 (0) | 2022.10.31 |
| [ML] 분류 (2) - 다중 분류 (0) | 2022.10.27 |