● 퍼셉트론
1. 초기 머신러닝의 역사
- Warren McCulloch과 Walter Pits가 뇌의 뉴런 개념을 발표
(MCP 뉴런 - 신경 세포를 이진 출력을 내는 간단한 논리 회로로 표현)
- Frank Rosenblatt는 MCP 뉴런 모델을 기반으로 퍼셉트론 학습 개념을 발표
- 퍼셉트론 규칙에서 자동으로 최적의 가중치를 학습하는 알고리즘 제안
- 가중치는 뉴런의 출력 신호를 낼지 말지 결정하기 위해 입력 특성에 곱하는 계수
- 지도학습과 분류 문제에서 퍼셉트론 알고리즘을 사용하여 새로운 데이터가 한 클래스에 속하는지 아닌지 예측 가능
2. 인공 뉴런의 수학적 정의
- 두 클래스를 1과 -1로 나타냄
- 입력값 \(x\)와 가중치 벡터 \(w\)의 선형 조합으로 결정함수 \(\phi(z)\) 정의
$$z = w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{m}x_{m}$$
$$w = \begin{bmatrix} w_{1} \\ \vdots \\ w_{m} \end{bmatrix}, x= \begin{bmatrix} x_{1} \\ \vdots \\ x_{m} \end{bmatrix}$$
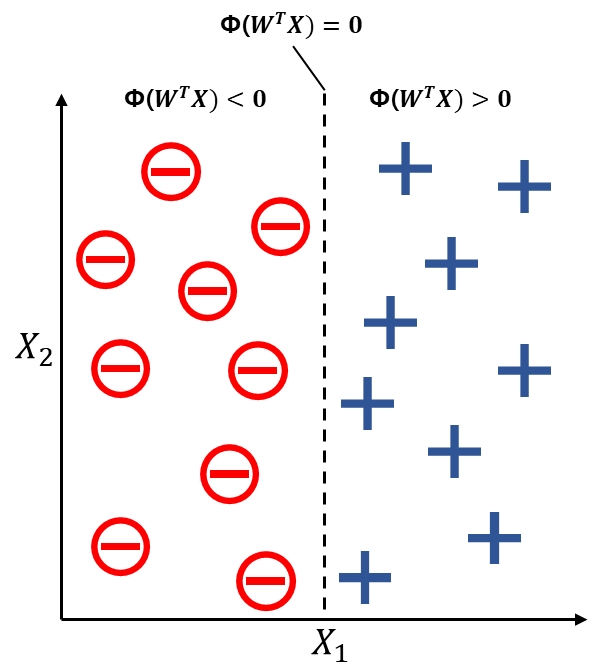
- 특정 샘플 \(x\)의 최종 입력이 사전 정의된 임계값 \(\theta\)보다 크면 클래스 1, 아니면 클래스 -1로 예측
$$\phi(z) = \begin{cases} 1 & z \geq \theta \\ -1 & 그외 \end{cases}$$
- \(z \geq \theta\) 식에서 \(\theta\)를 왼쪽으로 넘겨 \(w_{0}=-\theta\)이고, \(x_{0}=1\)인 0번째 가중치를 정의하여 식 간소화
$$z = w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{m}x_{m} = w^{T}x$$
- 결정함수는 다음과 같이 변경
$$\phi(z) = \begin{cases} 1 & z \geq 0 \\ -1 & 그외 \end{cases}$$
- \(w_{0} = -\theta\)를 절편이라고 함

3. 퍼셉트론 학습 규칙
- 뇌의 뉴런 하나가 작동하는 방식을 흉내내는 환원주의 접근 방식 사용
- 가중치를 0 또는 랜덤한 작은 값으로 초기화
- 각 훈련 샘플 \(x^{(i)}\)에서 다음 작업 수행
- 출력 값 \(\hat{y}\) 계산
→ 출력값은 계단 함수로 예측한 클래스 레이블 - 가중치 업데이트
→ \(w_{j}:=w_{j}+\Delta w_{j}\)
→ 가중치 업데이트 값인 \(\Delta w_{j}=\eta (y^{(i)}-\hat{y}^{(i)})x_{j}^{(i)}\)
→ \(\eta\)는 학습률로 0.0~0.1 사이의 값
→ \(y^{(i)}\)와 \(\hat{y}^{(i)}\)는 각각 \(i\)번째 훈련 샘플의 정답 레이블, 예측 레이블
- 출력 값 \(\hat{y}\) 계산
- 가중치 벡터의 모든 가중치는 동시에 업데이트
- 모든 가중치가 각자의 업데이트 값 \(\Delta w_{j}\)에 의해 업데이트되기 전에 예측 레이블 \(\hat{y}^{(i)}\)를 다시 계산하지 않음
→ \(\Delta w_{0}=\eta(y^{(i)}-output^{(i)})\)
→ \(\Delta w_{1}=\eta(y^{(i)}-output^{(i)})x_{1}^{(i)}\)
→ \(\Delta w_{2}=\eta(y^{(i)}-output^{(i)})x_{2}^{(i)}\)
- 퍼셉트론이 클래스 레이블을 정확히 예측하면 가중치 유지(업데이트 값은 0)
→ \(y^{(i)}=-1, \hat{y}^{(i)}=-1, \Delta w_{j}=\eta(-1-(-1))x_{j}^{(i)}=0\)
→ \(y^{(i)}=1, \hat{y}^{(i)}=1,\Delta w_{j}=\eta(1-1)x_{j}^{(i)}=0\)
- 퍼셉트론이 클래스 레이블을 잘못 예측하면 가중치를 양성 또는 음성 타겟 클래스 방향으로 이동시킴
→ \(y^{(i)}=1, \hat{y}^{(i)}=-1, \Delta w_{j}=\eta(1-(-1))x_{j}^{(i)}=\eta(2)x_{j}^{(i)}\)
→ \(y^{(i)}=-1, \hat{y}^{(i)}=1, \Delta w_{j}=\eta(-1-1)x_{j}^{(i)}=\eta(-2)x_{j}^{(i)}\)
- 가중치 업데이트는 \(x_{j}^{(i)}\)값에 비례하여, 이 값을 조절해 결정경계를 더 크게 움직이거나 더 작게 움직일 수 있음
- 퍼셉트론은 두 클래스가 선형적으로 구분되고 학습률이 충분히 작을 때만 수렴이 보장됨
- 선형 결정 경계로 나눌 수 없다면 훈련 데이터셋을 반복할 최대 횟수(epoch)를 지정해 분류 허용 오차 지정, 그렇지 않으면 퍼셉트론은 가중치 업데이트를 멈추지 않음

4. 파이썬으로 퍼셉트론 학습 알고리즘 구현
- 퍼셉트론 클래스 정의
import numpy as np
class Perceptron(object):
def __init__(self, eta = 0.01, n_iter = 50, random_state = 1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
rgen = np.random.RandomState(self.random_state) # 난수 생성기 객체 생성(격리된 시드 부여 가능, 이전과 동일한 랜덤 시드 재현 가능)
self.w_ = rgen.normal(loc = 0.0, scale = 0.01,
size = 1 + X.shape[1]) # 평균 0, 표준편차 0.01의 정규분포에서 훈련 데이터 개수(X.shape[1]) + 절편(1)만큼의 난수 생성
self.errors_ = [] # 훈련 중 error의 감소 확인을 위한 객체
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi)) # 가중치 w_j의 변화량
self.w_[1:] += update * xi # 각 훈련 데이터에 가중치값 곱하기
self.w_[0] += update # 가중치값 업데이트
errors += int(update != 0.0) # 업데이트 된 값이 0이 아니면(실제값과 예측값이 다르면) errors에 1 더함
self.errors_.append(errors) # 전체 훈련 데이터에서 예측값이 실제값과 다르게 나온 횟수 추가
return self
# 최종입력인 Z 계산
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
# 결정함수를 임계값인 0과 비교, 크거나 같으면 1, 작으면 -1로 반환
def predict(self, X):
return np.where(self.net_input(X) >= 0, 1, -1) - fit 메서드 내의 w_객체에 가중치를 초기화하여 선언
- 가중치가 0이 아니어야 학습률(eta)가 분류 결과에 영향을 줄 수 있어 0이 아닌 랜덤 값으로 초기화
- 가중치가 0이면 eta는 가중치 벡터의 방향이 아니라 크기에만 영향을 미침
- 붓꽃 데이터셋에서 퍼셉트론 훈련
- Perceptron은 이진분류이므로 setosa와 versicolor에 대해서만 분류 진행
- 또한, 특성은 첫번째 특성(꽃받침 길이)와 세번째 특성(꽃잎 길이)을 사용
import pandas as pd
import matplotlib.pyplot as plt
s = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
df = pd.read_csv(s, header = None, encoding = 'utf-8')
# 처음 100개의 데이터(setosa 50개와 versicolor 50개)의 다섯번째 열인 예측 대상을 y로 선언
y = df.iloc[0:100, 4].values
# setosa이면 -1, versicolor이면 1로 변경
y = np.where(y == 'Iris-setosa', -1, 1)
# 처음 100개의 데이터에서 예측에 사용하고자 하는 특성인 첫번재 열과 세번째 열만 추출
X = df.iloc[0:100, [0, 2]].values
# 산점도로 시각화
plt.scatter(X[:50, 0], X[:50, 1], color = 'red', marker = 'o', label = 'setose')
plt.scatter(X[50:100, 0], X[50:100, 1], color = 'blue', marker = 'x', label = 'versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc = 'upper left')
plt.show()
# Perceptron 알고리즘 훈련
ppn = Perceptron(eta = 0.1, n_iter = 10)
ppn.fit(X, y)
# 훈련 과정에서 각 반복에서 나온 오차의 개수 시각화
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker = 'o')
plt.xlabel('Epochs')
plt.ylabel('Number of updates')
plt.show()
from matplotlib.colors import ListedColormap
# 결정경계 시각화 함수
def plot_decision_regions(X, y, classifier, resolution = 0.02):
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# 두 특성의 최소값과 최대값에 각각 -1, +1을 한 값을 정의
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# 위에서 구한 최소값과 최대값을 시작으로 하는 meshgrid 생성(최소값과 최대값 사이에 0.02의 간격으로 데이터 생성)
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
# ravel 함수로 meshgrid를 1차원으로 평평하게 펴고, xx1, xx2를 각각 X, y로 Perceptron에 넣어 예측
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
# 예측된 값을 다시 meshgrid 형태로 변경
Z = Z.reshape(xx1.shape)
# contourf 함수로 등고선 그래프 그리기(등고선이 두 집단의 경계로 그려짐)
# 분류된 값이 -1인 것과 1인 것을 각각 빨간색과 파란색으로 구분
plt.contourf(xx1, xx2, Z, alpha = 0.3, cmap = cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# 훈련 데이터를 빨간색 네모 모양와 파란색 x모양으로 구분
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x = X[y == cl, 0], y = X[y == cl, 1],
alpha = 0.8, c = colors[idx], marker = markers[idx], label = cl, edgecolor = 'black')
plot_decision_regions(X, y, classifier = ppn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc = 'upper left')
plt.show()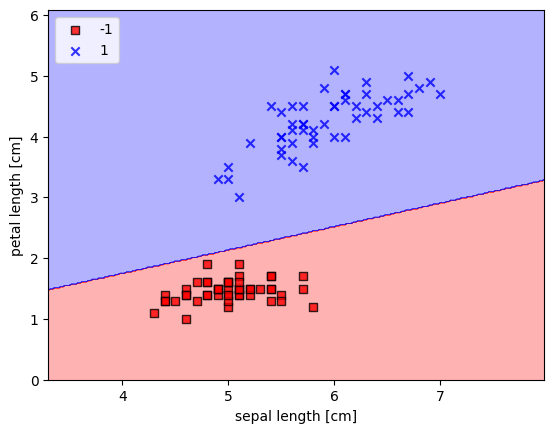
- OvR(One-versus-Resr)기법을 사용하면 이진 분류기로 다중 클래스 문제 해결 가능
→ 클래스마다 하나의 분류기를 훈련(각 클래스를 양성으로 분류하고 나머지는 음성으로 분류)
→ 레이블이 없는 새로운 데이터 샘플 분류 시에는 클래스 레이블의 개수와 같은 n개의 분류기 사용
→ 신뢰도가 가장 높은 클래스 레이블(최종 입력의 절댓값이 가장 큰 클래스)을 분류하려는 샘플의 레이블로 선택
- 퍼셉트론의 가장 큰 문제는 수렴
→ 구 클래스가 선형적인 초평면으로 구분될 수 있을 때 수렴하지만, 선형 결정 경계로 완벽하게 구분되지 않으면 최대 epoch를 지정하지 않는한 가중치 업데이트가 멈추지 않음
'Python > Machine Learning' 카테고리의 다른 글
| 머신러닝 기본 과정(Dacon, Kaggle 분류 및 회귀분석 초기 EDA 및 Feature Engineering 용) (0) | 2023.09.03 |
|---|---|
| [머신러닝 알고리즘] 추천 시스템 (1) | 2023.03.03 |
| [머신러닝 알고리즘] 분해 (0) | 2023.03.03 |
| [머신러닝 알고리즘] 다양체 학습 (0) | 2023.03.03 |
| [머신러닝 알고리즘] 군집화 (1) | 2023.03.02 |