[머신러닝 알고리즘] 분해

2023. 3. 3. 18:13

● 분해(Decomposition)

큰 하나의 행렬을 여러 개의 작은 행렬로 분해
분해 과정에서 중요한 정보만 남게됨

라이브러리, 데이터 불러오기

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris, fetch_olivetti_faces
from sklearn.decomposition import PCA, IncrementalPCA, KernelPCA, SparsePCA
from sklearn.decomposition import TruncatedSVD, DictionaryLearning, FactorAnalysis
from sklearn.decomposition import FastICA, NMF, LatentDirichletAllocation
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

iris, labels = load_iris(return_X_y = True)
faces, _ = fetch_olivetti_faces(return_X_y = True, shuffle = True)

iris 그래프 그리기 함수

def plot_iris(iris, labels):
    plt.figure()
    colors = ['navy', 'purple', 'red']
    for xy, label in zip(iris, labels):
        plt.scatter(xy[0], xy[1], color = colors[label])

faces 그리기 함수

def show_faces(faces):
    plt.figure()
    # 2*3의 배열로 표현
    num_rows, num_cols = 2, 3
    # 총 6개씩 뜨게 됨
    for i in range(num_rows * num_cols):
        plt.subplot(num_rows, num_cols, i+1)
        plt.imshow(np.reshape(faces[i], (64, 64)), cmap = plt.cm.gray)

위의 함수 사용해서 그래프 그리기

plot_iris(iris[:, :2], labels)

show_faces(faces)

1. 주성분 분석(Principal Component Analysis, PCA)

PCA를 사용해 iris 데이터 변환
150×4 크기의 데이터를 150×2 크기의 행렬로 압축

# 기존 iris 데이터의 shape
iris.shape

# 출력 결과
(150, 4)


# PCA 변환 후 iris 데이터의 shape
model = PCA(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# PCA로 변환한 iris 데이터 시각화
plot_iris(transformed_iris, labels)

PCA를 통해 학습된 각 컴포넌트(6개)
각 컴포넌트는 얼굴의 주요 특징을 나타냄

# 기존 faces 데이터의 shape
faces.shape

# 출력 결과
(400, 4096)


# PCA 변환 후 faces 데이터의 shape
model = PCA(n_components = 6, random_state = 0)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# PCA로 변환한 faces 데이터 시각화
show_faces(faces_components)

2. Incremental PCA

PCA는 SVD 알고리즘 실행을 위해 전체 학습용 데이터 셋을 메모리에 올려야 함
Incremental PCA는 학습 데이터를 미니 배치 단위로 나누어 사용
학습 데이터가 크거나 온라인으로 PCA 적용이 필요할 때 유용

model = IncrementalPCA(n_components = 2)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)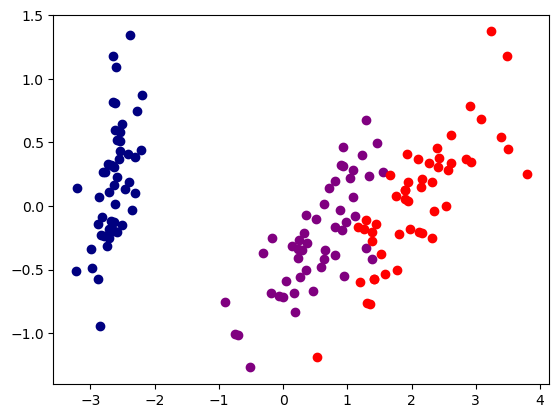

model = IncrementalPCA(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

3. Kernel PCA

비선형적인 형태가 Kernel로 표현될 수 있음
차원 축소를 위한 복잡한 비선형 투형

model = KernelPCA(n_components = 2, kernel = 'rbf', random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)

model = KernelPCA(n_components = 6)
model.fit(faces)

# Kernel PCA는 components_를 출력할 수 없어 오류가 발생함
faces_components = model.components_

4. Sparse PCA

PCA의 주요 단점 중 하나는 주성분들이 보통 모든 입력 변수들의 선형 결합으로 나타난다는 점
희소 주성분 분석은 몇 개의 변수들만의 선형결합으로 주성분을 나타냄으로써 이러한 단점을 극복

model = SparsePCA(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)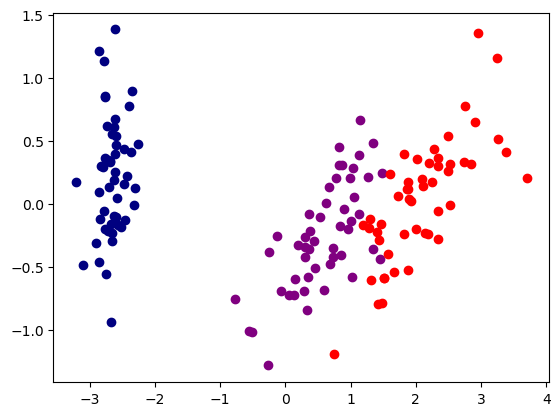

model = SparsePCA(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

5. Truncated Singular Value Decomposition(Truncated SVD)

PCA는 정방 행렬에 대해서만 행렬 분해 가능
SVDs는 정방 행렬 뿐만 아니라 행과 열이 다른 행렬도 분해 가능
PCA는 밀집 행렬(Dense Matrix)에 대한 변환만 가능하지만, SVD는 희소 행렬(Sparse Matrix)에 대한 변환도 가능
전체 행렬 크기에 대해 Full SVD를 사용하는 경우는 적음
특이값이 0인 부분을 모두 제거하고 차원을 줄인 Truncated SVD를 주로 사용

model = TruncatedSVD(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)

model = TruncatedSVD(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

6. Dictionary Learning

Sparse code를 사용하여 데이터를 가장 잘 나타내는 사전 찾기
Sparse coding은 overcomplete 기저 벡터(basis vector)(기저보다 많은 수의 함수로 프레임 표현하는 )를 기반으로 데이터를 효율적으로 표현하기 위한 개발
기저 벡터는 벡터 공간에 속하는 벡터의 집합이 선형 독립이고, 다른 모든 벡터 공간의 벡터들이 그 벡터 집합의 선형 조합으로 나타남
이웃한 픽셀들의 가능한 모든 조합으로 이미지를 재정의
픽셀 정보를 넘어서 더 풍부한 표현력으로 이미지를 설명, 인식의 정확성 향상

model = DictionaryLearning(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)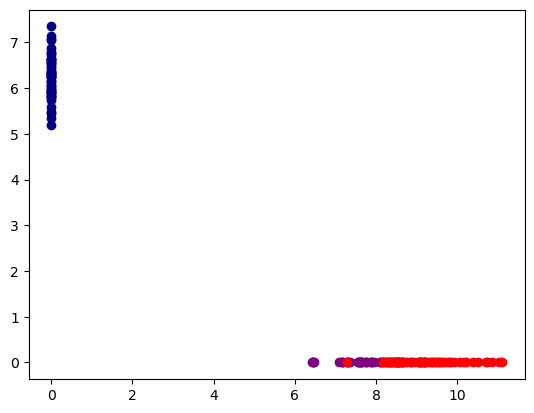

model = DictionaryLearning(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

7. Factor Analysis

요인 분석은 변수들 간의 상관관계를 고려하여 저변에 내재된 개념인 요인들을 추출해내는 분석방법
요인 분석은 변수들 간의 상관관계를 고려하여 서로 유사한 변수들끼지 묶어주는 방법
PCA에선느 오차(error)를 고려하지 않고, 요인 분석에서는 오차(error)를 고려

model = FactorAnalysis(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)

model = FactorAnalysis(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

8. Independent Component Analysis(ICA)

독립 성분 분석은 다변량의 신호를 통계적으로 독립적인 하부 성분으로 분리하는 계산 방법
ICA는 주성분을 이용하는 점은 PCA와 유사하지만, 데이터를 가장 잘 설명하는 축을 찾는 PCA와 달리 가장 독립적인 축, 독립성이 최대가 되는 벡터를 찾음

model = FastICA(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)

model = FastICA(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

9. Non-negative Matrix Factorization

음수 미포함 행렬 분해는 음수를 포함하지 않은 행렬 V를 음수를 포함하지 않은 행렬 W와 H의 곱으로 분해하는 알고리즘
숫자 5를 분해하면 2+3, 1+4 등으로 분리 가능 -> 이것과 마찬가지로 행렬을 어떤 두 개의 행렬의 곱으로 분해

model = NMF(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)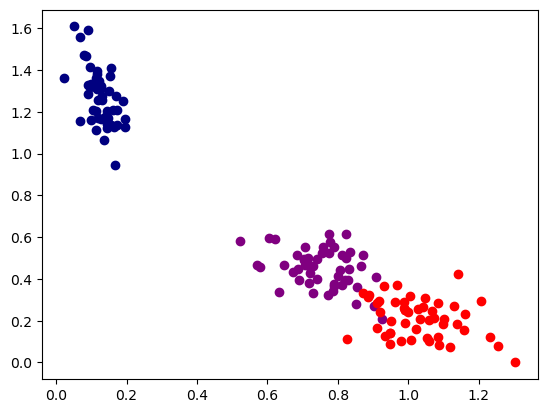

model = NMF(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

10. Latent Dirichlet Allocation(LDA)

잠재 디리클레 할당은 이산 자료들에 대한 확률적 생성 모형
디리클레 분포에 따라 잠재적인 의미 구조를 파악
- 디리클레 분포(Dirichlet distribution)는 연속 확률분포의 하나로, k차원의 실수 벡터 중 벡터의 요소가 양수이며 모든 요소를 더한 값이 1인 경우 (이를 k−1차원 단체라고 한다)에 대해 확률값이 정의되는 분포이다.
- 디리클레 분포는 베이즈 통계학에서 다항 분포에 대한 사전 켤레확률이다. 이 성질을 이용하기 위해, 디리클레 분포는 베이즈 통계학에서의 사전 확률로 자주 사용된다.

model = LatentDirichletAllocation(n_components = 2, random_state = 0)
model.fit(iris)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)

model = LatentDirichletAllocation(n_components = 6)
model.fit(faces)
faces_components = model.components_
faces_components.shape

# 출력 결과
(6, 4096)

# 시각화
show_faces(faces_components)

11. Linear Discriminant Analysis(LDA)

LDA는 PCA와 유사하게 입력 데이터 세트를 저차원 공간에 통해 차원을 축소
LDA는 지도 학습 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원 축소
정답이 있는 지도학습에서 사용하기 때문에 faces 데이터에 대해서는 사용 불가능

model = LinearDiscriminantAnalysis(n_components = 2)
# 정답인 labels를 같이 모델에 넣어 학습시켜 줘야함
model.fit(iris, labels)
transformed_iris = model.transform(iris)
transformed_iris.shape

# 출력 결과
(150, 2)

# 시각화
plot_iris(transformed_iris, labels)

12. 압축된 표현을 사용한 학습

원래의 digits 데이터와 분해(decomposition)된 digits 데이터의 cross val score 비교

- digits 데이터 및 학습 모델 라이브러리 불러오기

from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import cross_val_score

# min_max 스케일링 하는 함수
def min_max_scale(x):
    min_value, max_value = np.min(x, 0), np.max(x, 0)
    x = (x - min_value) / (max_value - min_value)
    return x
    
# digits 데이터 그래프 그리는 함수
def plot_digits(digits, labels):
    digits = min_max_scale(digits)
    ax = plt.subplot(111, projection = '3d')
    for i in range(digits.shape[0]):
        ax.text(digits[i, 0], digits[i, 1], digits[i, 2],
                str(labels[i]), color = plt.cm.Set1(labels[i] / 10.),
                fontdict = {'weight': 'bold', 'size': 9})
    ax.view_init(4, -72)

# digits 데이터 불러온 뒤 NMF로 분해
# 기존 데이터와 분해된 데이터 shape 비교
digits = load_digits()
nmf = NMF(n_components = 3)
nmf.fit(digits.data)
decomposed_digits = nmf.transform(digits.data)
print(digits.data.shape)
print(decomposed_digits.shape)
print(decomposed_digits)

# 출력 결과
(1797, 64)
(1797, 3)
[[0.48392621 0.         1.24523912]
 [0.5829615  1.4676756  0.07150889]
 [0.61515882 1.10963207 0.387782  ]
 ...
 [0.55272665 1.26056519 0.72094739]
 [0.7872562  0.2789873  1.04952028]
 [0.78507412 0.67250884 0.92677982]]

# 시각화
plt.figure(figsize = (20, 10))
plot_digits(decomposed_digits, digits.target)

- KNN

# 분해 전
knn = KNeighborsClassifier()
score = cross_val_score(
    estimator = knn,
    X = digits.data, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.94722222 0.95555556 0.96657382 0.98050139 0.9637883 ]
mean cross val score: 0.9627282575054161 (+/- 0.011168537355954218)


# 분해 후
knn = KNeighborsClassifier()
score = cross_val_score(
    estimator = knn,
    X = decomposed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.54722222 0.58055556 0.64066852 0.59610028 0.56267409]
mean cross val score: 0.5854441349427422 (+/- 0.03214521445075084)

- SVC

# 분해 전
svm = SVC()
score = cross_val_score(
    estimator = svm,
    X = digits.data, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.96111111 0.94444444 0.98328691 0.98885794 0.93871866]
mean cross val score: 0.9632838130609718 (+/- 0.02008605863225686)

# 분해 후
svm = SVC()
score = cross_val_score(
    estimator = svm,
    X = decomposed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.61388889 0.62222222 0.66016713 0.60167131 0.59888579]
mean cross val score: 0.6193670690188796 (+/- 0.022070024720937543)

- Decision Tree

# 분해 전
decision_tree = DecisionTreeClassifier()
score = cross_val_score(
    estimator = decision_tree,
    X = digits.data, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.78333333 0.69722222 0.78830084 0.83286908 0.78830084]
mean cross val score: 0.7780052615289385 (+/- 0.04421837659784472)


# 분해 후
decision_tree = DecisionTreeClassifier()
score = cross_val_score(
    estimator = decision_tree,
    X = decomposed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.57222222 0.50833333 0.57938719 0.5821727  0.52924791]
mean cross val score: 0.5542726709996905 (+/- 0.0298931375955385)

- Random Forest

# 분해 전
random_forest = RandomForestClassifier()
score = cross_val_score(
    estimator = random_forest,
    X = digits.data, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.93888889 0.90555556 0.97214485 0.96657382 0.91086351]
mean cross val score: 0.9388053234292789 (+/- 0.02745509790638632)


# 분해 후
random_forest = RandomForestClassifier()
score = cross_val_score(
    estimator = random_forest,
    X = decomposed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.58888889 0.60277778 0.64066852 0.59052925 0.54874652]
mean cross val score: 0.594322191272052 (+/- 0.029463634023029848)

- 전반적으로 분해한 데이터에서 성능이 떨어진 모습

13. 복원된 표현을 사용한 학습

분해 후 복원된 행렬을 사용해 학습

- 데이터 행렬 복원

# 분해된 행렬에 곱하기 연산을 통해 원래의 행렬로 복원
components = nmf.components_
reconstructed_digits = decomposed_digits @ components
print(digits.data.shape)
print(decomposed_digits.shape)
print(reconstructed_digits.shape)

# 출력 결과
(1797, 64)
(1797, 3)
(1797, 64)

# reconstructed digits 시각화
plt.figure(figsize = (16, 8))
plt.suptitle('Re-Constructed digits')
for i in range(10):
    plt.subplot(2, 5, i+1)
    plt.xticks([])
    plt.yticks([])
    plt.imshow(reconstructed_digits[i].reshape(8, 8))

- KNN

knn = KNeighborsClassifier()
score = cross_val_score(
    estimator = knn,
    X = reconstructed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.54166667 0.59444444 0.66295265 0.57660167 0.57381616]
mean cross val score: 0.5898963169297431 (+/- 0.04029722337499952)

- SVM

svm = SVC()
score = cross_val_score(
    estimator = svm,
    X = reconstructed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.62777778 0.60555556 0.66016713 0.61002786 0.5821727 ]
mean cross val score: 0.6171402042711235 (+/- 0.025969174809053776)

- Decision Tree

decision_tree = DecisionTreeClassifier()
score = cross_val_score(
    estimator = decision_tree,
    X = reconstructed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.57777778 0.51666667 0.53481894 0.56824513 0.55153203]
mean cross val score: 0.5498081089445992 (+/- 0.0221279380012718)

- Random Forest

random_forest = RandomForestClassifier()
score = cross_val_score(
    estimator = random_forest,
    X = reconstructed_digits, y = digits.target,
    cv = 5
)
print(score)
print('mean cross val score: {} (+/- {})'.format(score.mean(), score.std()))

# 출력 결과
[0.58055556 0.55833333 0.65181058 0.59610028 0.57660167]
mean cross val score: 0.592680284741566 (+/- 0.031916555892366645)

- 새로 복원한 데이터에서도 큰 성능 향상점은 없음

14. 이미지 복원

# faces 데이터를 train와 test 데이터로 분리
from sklearn.model_selection import train_test_split

train_faces, test_faces = train_test_split(faces, test_size = 0.1)
show_faces(train_faces)

show_faces(test_faces)

# 테스트 데이터에는 랜덤한 점에 0값을 주어 검은색의 점으로 노이즈를 생성
damaged_faces = []
for face in test_faces:
    idx = np.random.choice(range(64 * 64), size = 1024)
    damaged_face = face.copy()
    damaged_face[idx] = 0.
    damaged_faces.append(damaged_face)
show_faces(damaged_faces)

# train 데이터로 NMF 분해 학습
nmf = NMF(n_components = 10)
nmf.fit(train_faces)

# 노이즈를 준 test 데이터를 NMF 모델에 넣어 분해하고 다시 복원하는 과정으로 노이즈 제거
# damaged_faces의 형식을 float32로 변환하는 과정 필요
damaged_faces = np.asarray(damaged_faces, dtype = np.float32)
matrix1 = nmf.transform(damaged_faces)
matrix2 = nmf.components_
show_faces(matrix1 @ matrix2)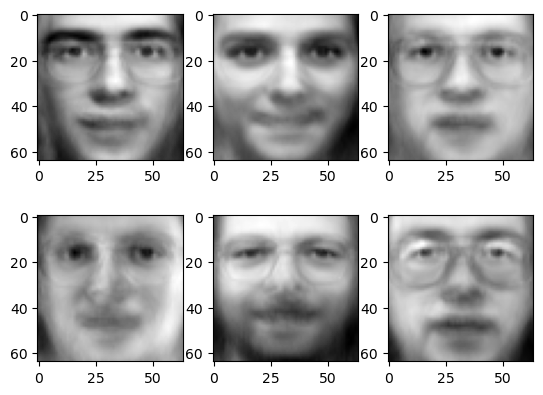

# 분해 components를 조절하여 정교함 조절 가능, 더 높은 수로 분해할수록 더 정교하게 복원할 수 있음
nmf = NMF(n_components = 100)
nmf.fit(train_faces)

matrix1 = nmf.transform(damaged_faces)
matrix2 = nmf.components_
show_faces(matrix1 @ matrix2)

nmf = NMF(n_components = 300)
nmf.fit(train_faces)

matrix1 = nmf.transform(damaged_faces)
matrix2 = nmf.components_
show_faces(matrix1 @ matrix2)

저작자표시

'Python > Machine Learning' 카테고리의 다른 글

머신러닝 기본 과정(Dacon, Kaggle 분류 및 회귀분석 초기 EDA 및 Feature Engineering 용) (0)	2023.09.03
[머신러닝 알고리즘] 추천 시스템 (1)	2023.03.03
[머신러닝 알고리즘] 다양체 학습 (0)	2023.03.03
[머신러닝 알고리즘] 군집화 (1)	2023.03.02
[머신러닝 알고리즘] XGBoost, LightGBM (0)	2023.02.23

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

감으로 코딩하던 내가 알고 코딩할 때까지

[머신러닝 알고리즘] 분해

'Python > Machine Learning' 카테고리의 다른 글

+ Recent posts

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역