[딥러닝 기초] 신경망 구조

1. 퍼셉트론

• 인공신경망의 한 종류
• 다수의 입력(\(x_{1}, x_{2}, x_{3}, \cdots, x_{n}\))과 가중치(\(w_{1}, w_{2}, w_{3}, \cdots, w_{n}\))를 곱하여 그 값에 편향(\(bias\))를 더한 값이 어느 임계치 값(\(\theta\))을 초과하면 활성화 함수를 통과한 출력값을 내보냄

https://towardsdatascience.com/rosenblatts-perceptron-the-very-first-neural-network-37a3ec09038a

 

2. 뉴런의 수학적 표현

https://cs231n.github.io/convolutional-networks/

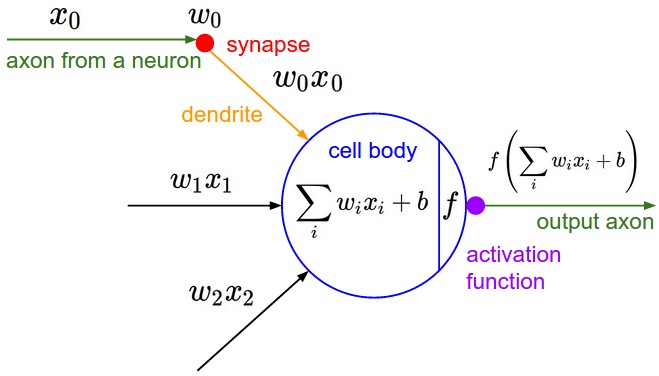
• 뉴런의 axon(\(x_{0}\))이 synapse를 통과하며 가중치(\(w_{0}\))가 주어짐 → dendrite를 통해 \(w_{0}x_{0}\)이 cell body에 들어감 → 이외에 \(w_{1}x_{1}\), \(w_{2}x_{2}\)등도 cell body에 들어옴
• cell body에서 값들이 합해지고, 합한 값에 마지막으로 편향을 더해줌 → activation function 과정을 거쳐 output axon으로 출력됨
• \(y=f(\sum _{i}w_{i}x_{i}+b)\)
• \(f\): 활성화 함수
  • 임계값(\(\theta\))을 경계로 출력이 바뀜
• \(b\): 편향
  • 결정 경계선을 원점에서부터 벗어나게 해줌
  • 따로 표현이 없어도 기본적으로 존재한다고 생각
• \(\sum _{i}w_{i}x_{i}\): 두 벡터의 내적으로 표현 가능
  \(x_{1}w_{1} + x_{2}w_{2} + \cdots + x_{n}w_{n} = w^{T}x\)

 

3. 완전 연결 계층(Fully-Connected Layer) 수학적 표현

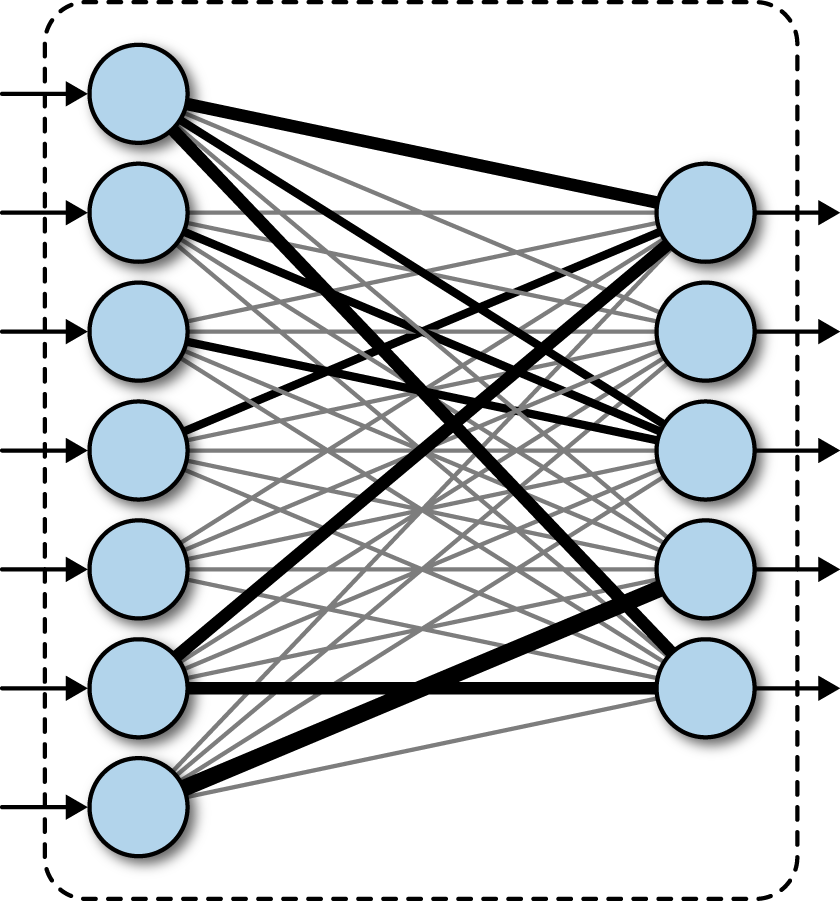
• 모드 노드들이 연결된 구조
• \(W=[w_{0}, w_{1}, \cdots, w_{M-1}]^{T}\)
  각각의 \(w_{k}\)는 \(N \times 1\) 형태의 벡터
  \(W\)는 \(N \times M\)행렬
  \(b=[b_{0}, b_{1}, \cdots, b_{M-1}]\\
  y_{0}=f(w_{0}^{T}x+b_{0})\\
  y_{1}=f(w_{1}^{T}x+b_{1})\\
  y_{2}=f(w_{2}^{T}x+b_{2})\\
  \cdots\\
  y_{M-1}=f(w_{M-1}^{T}x+b_{M-1})\\
  \to y=f(Wx+b)\)

 

4. 논리 회로

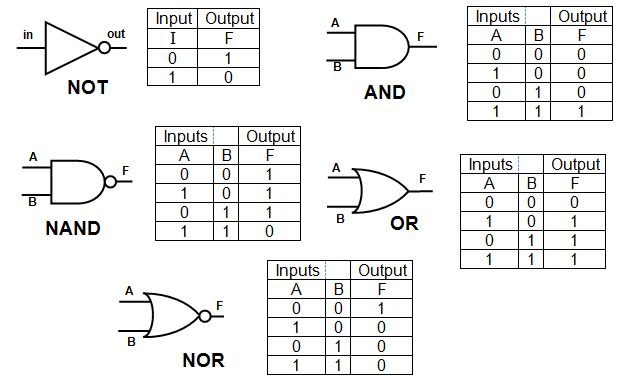
• 논리 게이트(Logic Gates)
  • AND: 둘 다 1이면 1
  • OR: 둘 중 하나면 1이면 1
  • NOT: 하나가 1이면 다른 하나는 0, 하나가 0이면 다른 하나는 1
  • NAND: 둘 다 1이면 0
  • NOR: 둘 다 0이면 1
• 다이어그램과 진리표

http://www.schoolphysics.co.uk/age14-16/Electronics/text/Logic_gates/index.html

 

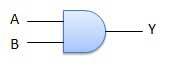
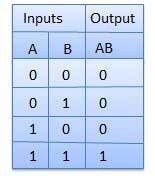
  - AND 게이터

• 두 입력이 모두 1일 때 1을 출력하는 논리회로

https://www.tutorialspoint.com/computer_logical_organization/logic_gates.htm

def AND(a, b):
    input = np.array([a, b])
    weights = np.array([0.4, 0.4])
    bias = -0.6
    value = np.sum(input * weights) + bias

    if (value <= 0):
        return 0
    else:
        return 1
        
print(AND(0, 0))  # 0
print(AND(0, 1))  # 0
print(AND(1, 0))  # 0
print(AND(1, 1))  # 1

x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = -0.6

y = (-0.4 * x1 - bias) / 0.4

plt.axvline(x = 0)
plt.axhline(y = 0)
plt.plot(x1, y, 'r--')
plt.scatter(0, 0, color = 'orange', marker = 'o', s = 150)
plt.scatter(0, 1, color = 'orange', marker = 'o', s = 150)
plt.scatter(1, 0, color = 'orange', marker = 'o', s = 150)
plt.scatter(1, 1, color = 'black', marker = '^', s = 150)
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1.5)
plt.grid()
plt.show()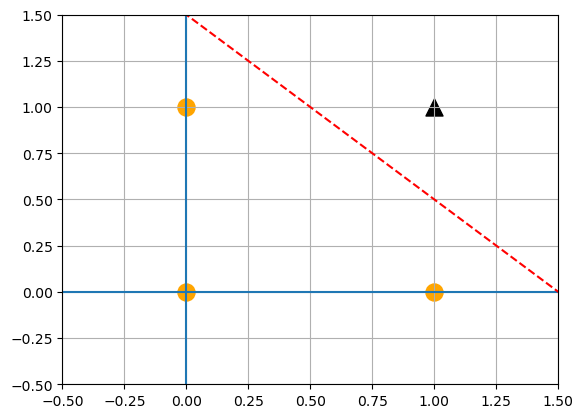

• 빨간선인 임계값을 넘어간 부분이 결과 1을 출

 

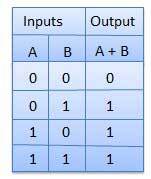
  - OR 게이트

• 두 입력 중 하나라도 1이면 1을 출력하는 논리회로

https://www.tutorialspoint.com/computer_logical_organization/logic_gates.htm

def OR(a, b):
    input = np.array([a, b])
    weights = np.array([0.4, 0.5])
    bias = -0.3
    value = np.sum(input * weights) + bias

    if (value <= 0):
        return 0
    else:
        return 1

print(OR(0, 0))  # 0
print(OR(0, 1))  # 1
print(OR(1, 0))  # 1
print(OR(1, 1))  # 1

x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = -0.3

y = (-0.4 * x1 - bias) / 0.5

plt.axvline(x = 0)
plt.axhline(y = 0)
plt.plot(x1, y, 'r--')
plt.scatter(0, 0, color = 'orange', marker = 'o', s = 150)
plt.scatter(0, 1, color = 'black', marker = '^', s = 150)
plt.scatter(1, 0, color = 'black', marker = '^', s = 150)
plt.scatter(1, 1, color = 'black', marker = '^', s = 150)
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1.5)
plt.grid()
plt.show()

• 빨간선인 임계값을 넘어간 부분이 결과 1을 출력

 

  - NAND 게이트

• 두 입력이 모두 1일 때 0을 출력하는 논리회로

https://www.tutorialspoint.com/computer_logical_organization/logic_gates.htm

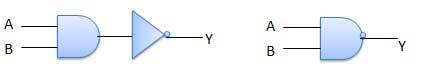
def NAND(a, b):
    input = np.array([a, b])
    weights = np.array([-0.6, -0.5])
    bias = 0.7
    value = np.sum(input * weights) + bias

    if (value <= 0):
        return 0
    else:
        return 1
        
print(NAND(0, 0))  # 1
print(NAND(0, 1))  # 1
print(NAND(1, 0))  # 1
print(NAND(1, 1))  # 0

x1 = np.arange(-2, 2, 0.01)
x2 = np.arange(-2, 2, 0.01)
bias = 0.7

y = (0.6 * x1 - bias) / -0.5

plt.axvline(x = 0)
plt.axhline(y = 0)
plt.plot(x1, y, 'r--')
plt.scatter(0, 0, color = 'black', marker = '^', s = 150)
plt.scatter(0, 1, color = 'black', marker = '^', s = 150)
plt.scatter(1, 0, color = 'black', marker = '^', s = 150)
plt.scatter(1, 1, color = 'orange', marker = 'o', s = 150)
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1.5)
plt.grid()
plt.show()

• 빨간선인 임계값을 넘어간 부분이 결과 0을 출력

 

5. XOR 게이트

• 인공지능 첫번째 겨울, 딥러닝의 첫번째 위기를 초래
• AND, NAND와 같은 선형 문제는 퍼셉트론으로 해결 가능하지만, XOR은 직선(선형) 하나로는 불가능
• 다층 퍼셉트론으로 해
• AND, NAND, OR Gate를 조합

 

6. 다층 퍼셉트론(Multi Layer Perceptron, MLP)

  - 다층 퍼셉트론의 구성

• 입력층(input layer)
• 은닉층(hidden layer)
  • 1개 이상 존재
  • 보통 5개 이상 존재하면 Deep Neural Network라고 칭함
• 출력층(output layer)

https://www.researchgate.net/figure/A-schematic-diagram-of-artificial-neural-network-and-architecture-of-the-feed-forward_fig1_26614896

• 수식
  • (input layer → hidden layer)
    \(z=f_{L}(W_{L}x+b_{L})\)
  • (hidden layer → output layer)
    \(y=a_{K}(W_{K}z+b_{K})\)

 

  - XOR 게이트

• 서로 다른 두 값이 입력으로 들어가면 1을 반환

https://www.tutorialspoint.com/computer_logical_organization/logic_gates.htm

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

print(XOR(0, 0))  # 0
print(XOR(0, 1))  # 1
print(XOR(1, 0))  # 1
print(XOR(1, 1))  # 0

 

7. 활성화 함수(Activation Function)

• 입력 신호의 총합을 출력 신호로 변환하는 함수
• 활성화 함수에 따라 출력값이 결정
• 단층, 다층 퍼셉트론 모두 사용
• 대표적인 활성화 함수
  • Sigmoid
  • ReLU
  • tanh
  • Identify Function
  • Softmax
• 하나의 layer에서 다음 layer로 넘어갈 때는 항상 활성화 함수를 통과

 

  - 계단 함수(Step Function)

• \(y=\begin{cases}
   0&(x<0)  \\
   1& (x\geq 0)
  \end{cases}\)

https://www.intmath.com/laplace-transformation/1a-unit-step-functions-definition.php

def step_function(x):
    if x > 0:
        return 1
    else:
        return 0

def step_function_for_numpy(x):
    y = x > 0
    return y.astype(int)


print(step_function(-3))   # 0
print(step_function(5))    # 1

# 넘파이 배열로 입력값을 줄 때 사용
a = np.array([5, 3, -4, 2.0])
print(step_function_for_numpy(a))   # [1 1 0 1]

 

  - 시그모이드 함수(Sigmoid Function)

• 이진분류(binary Classification)에 주로 사용
  • 마지막 출력층의 활성화 함수로 사용
• 출력값이  0~1의 값이며, 이는 확률로 표현 가능
  \(y=\frac{1}{1+e^{-x}}\)

https://www.geeksforgeeks.org/implement-sigmoid-function-using-numpy/

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

print(sigmoid(3))   # 0.9525741268224334, 1에 근접
print(sigmoid(-3))  # 0.04742587317756678, 0에 근접

 

  - 시그모이드 함수와 계단 함수 비교

• 공통점
  • 출력값이 0~1내의 범위
  • 입력값의 정도에 따라 출력값의 정도가 달라짐 즉, 입력이 중요하면(입력값이 크면) 큰 값을 출력
• 차이점
  계단함수에 비해 시그모이드 함수는
  • 입력에 따라 출력이 연속적으로 변화
  • 출력이 '매끄러움'
    이는 모든 점에서 미분 가능함을 의미

plt.grid()
x = np.arange(-5.0, 5.0, 0.01)
y1 = sigmoid(x)
y2 = step_function_for_numpy(x)
plt.plot(x, y1, 'r--', x, y2, 'b--')
plt.show()

 

  - ReLU(Rectified Linear Unit)

• 가장 많이 쓰이는 함수 중 하나

• \(y=\begin{cases}
   0&(x\leq0)  \\
   x& (x> 0)
  \end{cases}\)

https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/

def ReLU(x):
    if x > 0:
        return x
    else:
        return 0

print(ReLU(5))   # 5
print(ReLU(-3))  # 0

 

  - 하이퍼볼릭 탄젠트 함수(Hyperbolic tangent function, tanh)

• \(y=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}

https://www.researchgate.net/figure/Hyperbolic-tangent-activation-function_fig1_326279910

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

print(tanh(3))   # 0.9950547536867306
print(tanh(-3))  # -0.9950547536867306

 

  - 항등 함수(Identity Function)

• 회귀(Regression) 문제에서 주로 사용
  • 출력층의 활성화 함수로 활용
• \(y=x\)
• 입력값 그대로 출력하기 때문에 굳이 정의할 필요는 없지만 신경망 중간 레이어 흐름과 통일하기 위해 사용

https://math.info/Algebra/Identity_Function/

def identify_function(x):
    return x

print(identify_function(4))   # 4
print(identify_function(-1))  # -1

X = np.array([2, -3, 0.4])
print(identify_function(X))   # [ 2.  -3.   0.4]

 

  - Softmax

• 다중 클래스 분류에 사용(Multi Class Classification)
• 입력값의 영향을 크게 받음
  입력값이 크면 출력값도 큼
• 출력값을 확률에 대응 가능
• 출력값의 총합은 1
• 수식
  \(y_{k}=\frac{exp(a_{k})} {\sum_{i=1}exp(a_{i})}\)

https://medium.com/data-science-bootcamp/understand-the-softmax-function-in-minutes-f3a59641e86d

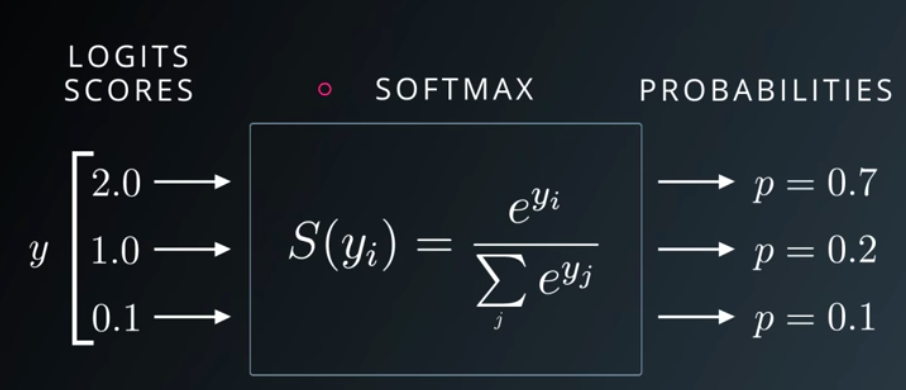
def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y

a = np.array([0.3, 0.2, 4.0, -1.2])
print(softmax(a))                 # [0.02348781 0.02125265 0.9500187  0.00524084]
print(np.sum(softmax(a)))    # 1.0

 

  - 소프트맥스 함수 주의점

• 오버플로우(overflow) 문제

A = np.array([1000, 900, 1050, 500])
print(softmax(A))

# 출력 결과
[nan nan nan  0.]
RuntimeWarning: overflow encountered in exp
  exp_a = np.exp(a)
RuntimeWarning: invalid value encountered in true_divide
  y = exp_a / sum_exp_a

• 지수 함수(exponential function)을 사용하지 때문에 입력값이 너무 크면 무한대(inf)가 반환됨
• 개선한 수식(C는 a의 최대값, 스케일링을 조금 하는 것)
  \(y_{k}=\frac {exp(a_{k})} {\sum_{i=1}exp(a_{i})} = \frac {Cexp(a_{k})} {C\sum_{i=1}exp(a_{i})}\\
  \quad = \frac {exp(a_{k} + logC)} {\sum_{i=1}exp(a_{i} + logC)}\\
  \quad = \frac {exp(a_{k}+C'} {\sum_{i=1}exp(a_{i}+C')}\)

def softmax(a):
    C = np.max(a)
    return (np.exp(a - C) / np.sum(np.exp(a - C)))

A = np.array([1000, 900, 1050, 500])
print(softmax(A))

# 출력 결과
[1.92874985e-022 7.17509597e-066 1.00000000e+000 1.37415257e-239]

 

  - 활성화 함수를 비선형 함수로 사용하는 이유

• 신경망을 깊게 하기 위함
• 만약 활성화 함수를 선형함수로 하게 되면 은닉층의 개수가 여러개이더라도 의미가 없어짐
• 만약, \(h(x)=cx\)이고, 3개의 은닉층이 존재한다면
  \(y=h(h(h(x)))\\
  \quad=c \times c \times c \times x\\
  \quad=c^{3}x\)
  이므로 결국 선형 함수가 되어버림

 

  - 그 외의 활성화 함수

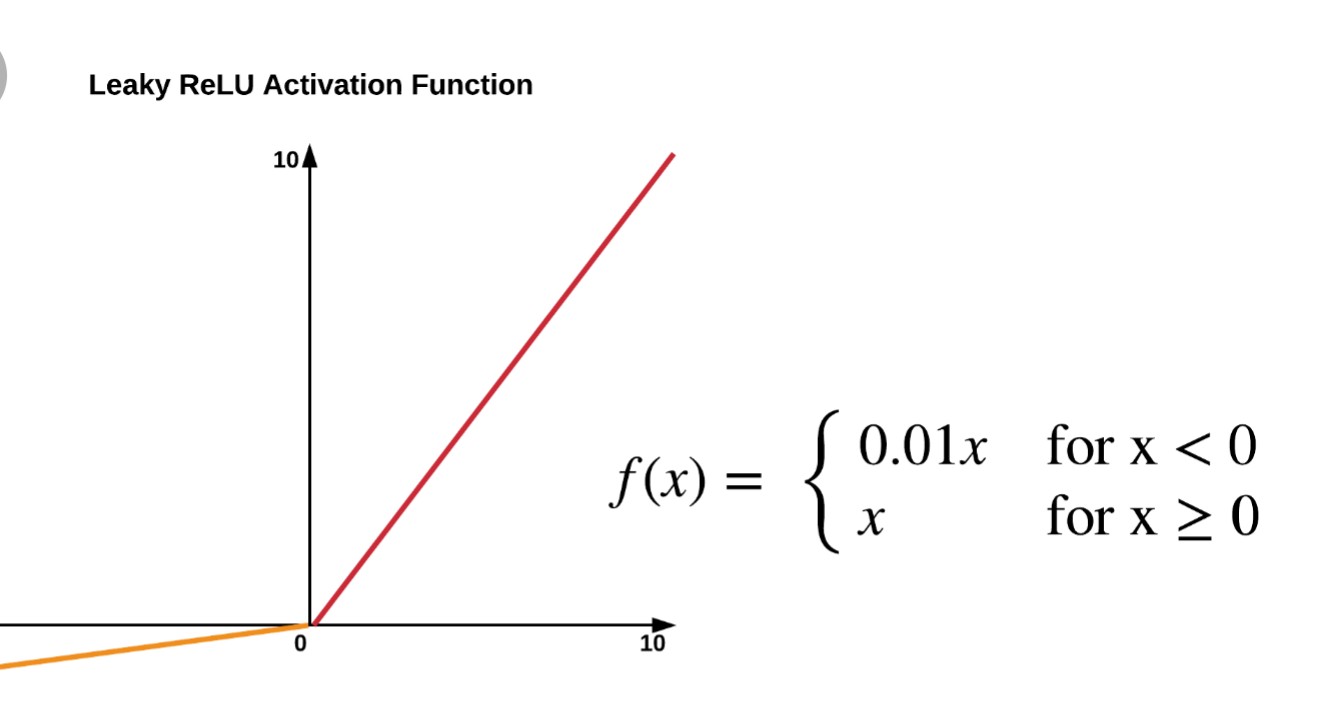
• LeakyReLU
• \(f_{a}(x)=\begin{cases}
   x& x \geq 0\\
   ax& x<0
  \end{cases}\)

https://knowhowspot.com/technology/ai-and-machine-learning/artificial-neural-network-activation-function/

def LeakyReLU(x):
    a = 0.01
    return np.maximum(a*x, x)
    
x = np.array([0.5, -1.4, 3, 0, 5])
print(LeakyReLU(x))

# 출력 결과
[ 0.5   -0.014  3.     0.     5.   ]

 

• ELU(Exponential Linear Units)
• \(f(\alpha, x)=\begin{cases}
   \alpha(e^{x}-1)& x \leq 0\\
   x& x>0
  \end{cases}\)

https://www.researchgate.net/figure/Exponential-Linear-Unit-activation-function-input-output-mapping-The-activation-function_fig1_331794632

def ELU(x):
    alpha = 1.0
    return ( x>= 0) * x + (x < 0) * alpha * (np.exp(x)-1)

print(ELU(4))       # 4.0
print(ELU(-0.5))   # -0.3934693402873666

x = np.array([-2, 0.1, 4])
print(ELU(x))      # [-0.86466472  0.1         4.        ]

 

  - 활성화 함수 참고

• 일반적인 사용 순서
  1. ELU
  2. LeakyReLU
  3. ReLU
  4. tanh
  5. sigmoid
• 스탠포드 강의에서 언급한 사용 순서
  1. ReLU
  2. ReLU Family(LeakyReLU, ELU)
  3. sigmoid는 사용 X

 

8. 3층 신경망 구현하기

• 2 클래스 분류
• 입력층(input layer)
  
  • 뉴런수: 3
• 은닉층(hidden layer)
  • 첫번째 은닉층 뉴런수: 3
  • 두번째 은닉층 뉴런수: 2
• 출력층(output layer)
  • 뉴런수: 2

 

  - 활성화 함수 정의

def sigmoid(X):
    return 1 / (1 + np.exp(-X))

X = np.array([1.0, 0.5, 0.4])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6], [0.3, 0.5, 0.7]])
B1 = np.array([1, 1, 1])

print(X.shape)    # (3,)
print(W1.shape)   # (3, 3)
print(B1.shape)   # (3,)

A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)

print(A1)
print(Z1)

# 출력 결과
[1.32 1.7  2.08]
[0.78918171 0.84553473 0.88894403]

# 두번째 레이어 통과
W2 = np.array([[0.2, 0.4, 0.6], [0.1, 0.3, 0.5], [0.4, 0.6, 0.8]])
B2 = np.array([1, 1, 1])

print(W2.shape)   # (3, 3)
print(B2.shape)   # (3,)

A2 = np.dot(A1, W2) + B2
Z2 = sigmoid(A2)

print(A2)
print(Z2)

# 출력 결과
[2.266 3.286 4.306]
[0.90602176 0.96394539 0.9866921 ]

# 세번째 레이어 통과
W3 = np.array([[0.1, 0.3], [-0.1, -0.5], [0.3, 0.5]])
B3 = np.array([1, 1])

print(W3.shape)   # (3, 2)
print(B3.shape)   # (2,)

A3 = np.dot(A2, W3) + B3
Z3 = sigmoid(A3)

print(A3)
print(Z3)

# 출력 결과
[2.1898 2.1898]
[0.8993298 0.8993298]

# 네번째 레이어 통과
W4 = np.array([[0.1, 0.2], [0.3, 0.5]])
B4 = np.array([1, 1])

print(W4.shape)   # (2, 2)
print(B4.shape)   # (2,)

A4 = np.dot(A3, W4) + B4
Z4 = sigmoid(A4)

print(A4)
print(Z4)

# 출력 결과
[1.87592 2.53286]
[0.86714179 0.92641356]

# 하나의 네트워크로 합치면 다음과 같이 됨
def network():
    network = {}

    # 첫번째 레이어
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6], [0.3, 0.5, 0.7]])
    network['B1'] = np.array([1, 1, 1])

    # 두번째 레이어
    network['W2'] = np.array([[0.2, 0.4, 0.6], [0.1, 0.3, 0.5], [0.4, 0.6, 0.8]])
    network['B2'] = np.array([1, 1, 1])

    # 세번째 레이어
    network['W3'] = np.array([[0.1, 0.3], [-0.1, -0.5], [0.3, 0.5]])
    network['B3'] = np.array([1, 1])

    # 네번째 레이어
    network['W4'] = np.array([[0.1, 0.2], [0.3, 0.5]])
    network['B3'] = np.array([1, 1])

    return network
    

def forward(network, x):
    W1, W2, W3, W4 = network['W1'], network['W2'], network['W3'], network['W4']
    B1, B2, B3, B4 = network['B1'], network['B2'], network['B3'], network['B4']

    A1 = np.dot(x, W1) + B1
    Z1 = sigmoid(A1)

    A2 = np.dot(Z1, W1) + B1
    Z2 = sigmoid(A2)

    A3 = np.dot(Z2, W1) + B1
    Z3 = sigmoid(A3)


    A4 = np.dot(Z3, W1) + B1
    y = sigmoid(A4)

    return y

  - 신경망 추론

net = network()
x = np.array([0.3, 1.3, -2.2])
y = forward(net, x)
print(y)

# 출력 결과
[0.78781193 0.82428264]