1. 지도 학습 vs 비지도 학습
- 지도 학습(Supervised Learning)
- 입력에 대한 정답(Label, Ground Truth)이 존재
- [입력-정답] 관계를 학습하여 새로운 입력에 대해 정답을 맞추는 과정
- 비지도 학습(Unsupervised Learning)
- 정답이 없음
- 데이터로부터 어떤 알고리즘을 통해 유용한 정보를 추출
2. 학습 매개변수(Trainable Parameter)
- 학습 매개변수: 학습 시, 값이 변화하는 매개변수, 이 매개변수에 따라 학습 알고리즘(모델)이 변함
- 학습 모델: 입력에 따른 출력을 나타내는 수식
선형회귀를 예로 들면,
$$ Y = aX + b $$- \(X\): 입력
- \(Y\): 출력
- \(a, b\): 학습 매개변수
- 초기화된 모델로부터 학습이 진행되면서 학습 데이터에 맞는 모델로 학습 파라미터를 수정해 나가는 과정

3. 하이퍼 파라미터(Hyper Parameter)
- 사람이 직접 설정해야하는 매개변수
- 학습이 되기 전 미리 설정되어 상수취급
- 손실함수(Cost Function)
- 학습률(Learnign Rate)
- 학습 반복 횟수(Epochs)
- 미니 배치 크기(Batch Size)
- 은닉층의 노드 개수(Units)
- 노이즈(Noise)
- 규제화(Regularization)
- 가중치 초기화(Weights Initialization)
- 신경망의 매개변수인 가중치는 학습 알고리에 의해 자동으로 갱
4. 손실함수(Loss Function, Cost Function)
- 학습이 진행되면서 해당 과정이 얼마 잘 되고 있는지 나타내는 지표
- 손실 함수에 따른 결를 통해 학습 파라미를 조정
- 최적화 이론에서 최소화하고자 하는 함수
- 미분 가능한 함수 사용

- 학습의 수학적 의미
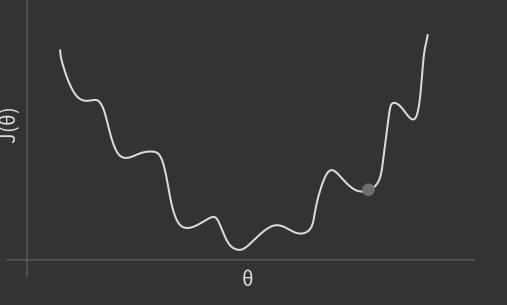
$$ \widetilde{\theta}=\underset{\theta}{argmin}L(x, y; \theta) $$
- \(L\): 손실함수
- \(x\): 학습에 사용되는 데이터의 입력값
- \(y\): 학습에 사용되는 데이터의 출력값
- \(\theta\): 학습될 모든 파라미를 모은 벡터
- \(\widetilde{\theta}\): 추정된 최적의 파라미터
- 학습에 사용되는 파라미터를 모두 통칭해서 \(\theta\)로 표현 가능, 이러한 \(\theta\)의 최적값을 찾는 것이 학습
- 학습 데이터의 입력(\(x\))와 \(\theta\)에 따라 나온 예측값이 정답(\y\)와 비교하여 \(\theta\)를 조절해나가는 과정
- 즉, 최적의 \(theta\)값에 따라 손실함수의 가정 최저점(최소값)을 찾는 과정
- 손실함수는 지도학습 알고리즘에 반드시 필요
5. 원-핫 인코딩
- 범주형 변수를 표현할 때 사용
- 가변수(Dummy Variable)이라고도 함
- 정답인 레이블을 제외하고 0으로 처리

import numpy as np
def convert_one_hot(labels, num_classes):
one_hot_result = np.zeros((len(labels), num_classes))
for idx, label in enumerate(labels):
one_hot_result[idx][label] = 1
return one_hot_result
x_label = [1, 3, 3, 4, 2, 0, 5, 3, 0]
print(convert_one_hot(x_label, max(x_label) + 1))
# 출력 결과
# 맨 앞에 0부터 시작
[[0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 1. 0.]
[0. 0. 1. 0. 0. 0.]
[1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 1.]
[0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 0.]]# Keras에서 원-핫 인코딩 하는 법
from keras.utils.np_utils import to_categorical
x_label = [1, 3, 3, 4, 2, 0, 5, 3, 0]
one_hot_label = to_categorical(x_label)
print(one_hot_label)
# 출력 결과
[[0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 1. 0.]
[0. 0. 1. 0. 0. 0.]
[1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 1.]
[0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 0.]]# sklearn에서 원-핫 인코딩
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelEncoder
def convert_one_hot_sklearn(class_label):
encoder = LabelEncoder()
encoder.fit(class_label)
labels = encoder.transform(class_label)
labels = labels.reshape(-1, 1)
oh_encoder = OneHotEncoder()
oh_encoder.fit(labels)
oh_labels = oh_encoder.transform(labels)
return oh_labels.toarray()
# 예시 데이터 생성
marvel_labels = ['아이언맨', '캡틴 아메리카', '헐크', '블랙 위도우', '스파이더맨', '앤트맨']
ohe = convert_one_hot_sklearn(marvel_labels)
print(ohe)
print("One hot encoder datatype:", type(ohe))
print("One hot encoder shape:", ohe.shape)
print("-----------------------------")
classes = [3, 2, 1, 3, 0, 4, 5, 3, 0]
ohe = convert_one_hot_sklearn(classes)
print(ohe)
print("One hot encoder datatype:", type(ohe))
print("One hot encoder shape:", ohe.shape)
# 출력 결과
[[0. 0. 1. 0. 0. 0.]
[0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 1.]
[1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]]
One hot encoder datatype: <class 'numpy.ndarray'>
One hot encoder shape: (6, 6)
-----------------------------
[[0. 0. 0. 1. 0. 0.]
[0. 0. 1. 0. 0. 0.]
[0. 1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 1.]
[0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 0.]]
One hot encoder datatype: <class 'numpy.ndarray'>
One hot encoder shape: (9, 6)# pandas에서 원-핫 인코딩
import pandas as pd
df = pd.DataFrame({'labels': ['아이언맨', '캡틴 아메리카', '헐크', '블랙 위도우', '스파이더맨', '앤트맨']})
ohe_df = pd.get_dummies(df['labels'])
ohe_df
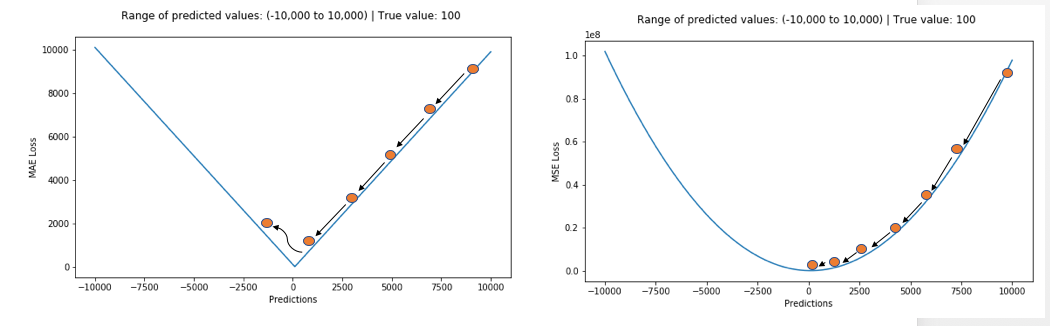
6. 평균절대오차(Mean Absolute Error, MAE)
- 오차가 커져도 손실함수가 일정하게 증가
- 이상치(Outlier)에 강건함(Robust)
- 데이터에서 [입력-정답]관계가 적절하지 않은 것이 있을 경우에, 좋은 추정을 하더라도 오차가 발생하는 경우가 발생
- 그때, 해당 이상치에 해당하는 지점에서 손실 함수의 최소값으로 가는 정도의 영향력이 크지 않음
- 중간값(Median)과 연관
- 회귀(Regression)에 많이 사용
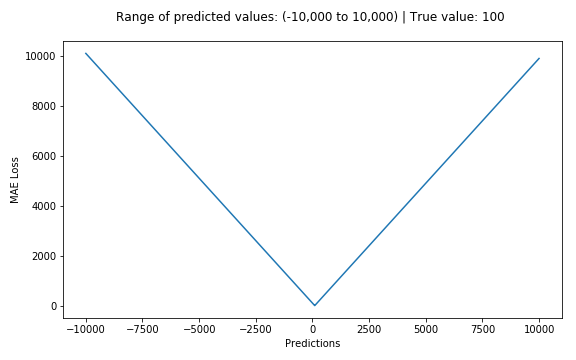
$$ E=\frac{1} {n} \sum_{i=1}^{n} \left |y_{i}-\widetilde{y_{i}} \right | $$
- \(y_{i}\): 학습 데이터의 \(i\)번째 정답
- \(\widetilde{y_{i}}\): 학습데이터의 입력으로 추정한 \(i\)번째 출력
def MAE(y, pred_y):
return np.mean(np.abs((y - pred_y)))
import matplotlib.pyplot as plt
y = np.array([-3, -1, -2, 1, 3, -2, 2, 5, 3, 3, -2, -1, 2])
yhat = np.array([-3, -1, -5, 0, 3, -1, 2, 4, 3, 3, -2, -1, -1])
x = list(range(len(y)))
plt.scatter(x, y, color = 'b', label = 'True')
plt.plot(x, yhat, color = 'r', label = 'Pred')
plt.legend()
plt.grid()
plt.show()
# 위 그래프와 같은 y와 y의 예측값을 가질 때 MAE 계산
print(MAE(y, yhat))
# 출력 결과
0.6923076923076923
7. 평균제곱오차(Mean Squared Error, MSE)
- 가장 많이 쓰이는 손실 함수 중 하나
- 오차가 커질수록 손실함수가 빠르게 증가
- 정답과 예측한 값의 차이가 클수록 더 많은 패널티를 부여
- 회귀(Regression)에 쓰임

$$ E=\frac{1} {n} \sum_{i=1}^{n} (y_{i}-\widetilde{y_{i}})^{2} $$
- \(y_{i}\): 학습 데이터의 \(i\)번째 정답
- \(\widetilde{y_{i}}\): 학습데이터의 입력으로 추정한 \(i\)번째 출력
def MSE(y, pred_y):
return 0.5 * np.sum(np.square(y - pred_y))
print(MSE(y, yhat))
# 출력 결과
10.5
- 손실함수로써의 MAE와 MSE 비교
8. 교차 엔트로피 오차(Cross Entropy Error, CEE)
- 이진 분류, 다중 클래스 분류
- 소프트맥스와 원-핫 인코딩 사이의 출력 간 거리를 비교
- 정답인 클래스에 대해서만 오차를 계산
- 정답을 맞추면 오차가 0, 틀리면 그 차이가 클수록 오차가 무한히 커짐
$$ E=-\frac{1}{N} \sum_{n} \sum_{i} y_{i} log\widetilde{y_{i}} $$
- \(y_{i}\): 학습 데이터의 \(i\)번째 정답
- \(\widetilde{y_{i}}\): 학습데이터의 입력으로 추정한 \(i\)번째 출력
- \(N\): 전체 데이터의 개수
- \(i\): 데이터 하나당 클래스 개수
- \(y=log(x)\)는
- \(x\)가 0에 가까울수록 \(y\)값은 무한히 커
- 1에 가까울수록 0에 가까워
- 정답 레이블(\(y_{i}\))은 원-핫 인코딩으로 정답인 인덱스에만 1이고, 나머지는 모두 0
- 따라서, 위 수식은 다음과 같이 나타낼 수 있음
$$ E=-log\widetilde{y_{i}} $$
- 소프트맥스를 통해 나온 신경망 출력이 0.6이라면 \(log0.6 \approx−0.51\)이 되고, 신경망 출력이 0.3이라면 \(−log0.3 \approx −1.2\)이 됨
- 정답에 가까워질수록 오차값은 작아짐
- 학습시, 원-핫 인코딩에 의해 정답 인덱스만 살아 남아 비교하지만, 정답이 아닌 인덱스들도 학습에 영향을 미침
다중 클래스 분류는 소프트맥스(softmax) 함수를 통해 전체 항들을 모두 다루기 때문

def CEE(y_pred, y_true):
delta = 1e-7
return -np.sum(y_true * np.log(y_pred + delta))
y = np.array([0, 0, 0, 0, 0, 1, 0, 0, 0, 0])
yhat = np.array([0.01, 0.1, 0.05, 0.0, 0.1, 0.7, 0.0, 0.03, 0.01, 0.0])
print("yhat 합:", np.sum(yhat))
print(CEE(yhat, y))
print("-----------------")
# yhat의 결과에서 0.03과 0.7 값의 위치를 바꿔 오차를 더 크게 만듦
y = np.array([0, 0, 0, 0, 0, 1, 0, 0, 0 ,0])
yhat = np.array([0.01, 0.1, 0.05, 0.0, 0.1, 0.03, 0.0, 0.7, 0.01, 0.0])
print("yhat 합:", np.sum(yhat))
print(CEE(yhat, y))
# 출력 결과
yhat 합: 1.0
0.3566748010815999
-----------------
yhat 합: 1.1
3.506554563992204
- 이진 분류에서의 교차 크로스 엔트로피(Binary Cross Entropy, BCE)
- 이진 분류 문제(Binary Classification Problem)에서도 크로스 엔트로피 오차를 손실함수로 사용 가능
$$ E = -\sum_{i=1}^{2} y_{i}log\widetilde{y_{i}} \\ \quad\qquad\qquad\qquad\qquad=-y_{1}log\widetilde{y}_{1}-(1-y_{1})log(1-\widetilde{y}_{1}) \\ \quad(\because y_{2}=1-y_{1}) $$
- \(y_{i}\): 학습 데이터의 \(i\)번째 정답
- \(\widetilde{y_{i}}\): 학습데이터의 입력으로 추정한 \(i\)번째 출력
- 2개의 클래스를 분류하는 문제에서 1번이 정답일 확률이 0.8이고, 실제로 정답이 맞다면 위 식은 다음과 같이 나타낼 수 있음
$$ E = -\sum_{i=1}^{2} y_{i}log\widetilde{y_{i}} \\ \quad\qquad\qquad\qquad\qquad=-1log0.8-(1-1)log(1-0.8) \\ =-log0.8 \\ \approx -0.22 $$
- 반대로 실제 정답이 2번이었다면, 식은 다음과 같이 나타낼 수 있음
$$ E = -\sum_{i=1}^{2} y_{i}log\widetilde{y_{i}} \\ \quad\qquad\qquad\qquad\qquad=-0log0.8-(1-0)log(1-0.8) \\=-log0.2 \\\approx -1.61 $$
# 2번이 정답
# 2번이 정답일 확률을 0.85로 예측, 맞음
y = np.array([0, 1])
yhat = np.array([0.15, 0.85])
print("yhat 합:", np.sum(yhat))
print(CEE(yhat, y))
print("-----------------")
# 1번이 정답
# 1번이 정답일 확률을 0.15로 예측, 틀림
y = np.array([1, 0])
yhat = np.array([0.15, 0.85])
print("yhat 합:", np.sum(yhat))
print(CEE(yhat, y))
# 출력 결과
yhat 합: 1.0
0.1625188118507231
-----------------
yhat 합: 1.0
1.8971193182194368'Python > Deep Learning' 카테고리의 다른 글
| [딥러닝 기초] 신경망 학습 (0) | 2023.03.14 |
|---|---|
| [딥러닝 기초] 경사하강법 (0) | 2023.03.13 |
| [딥러닝 기초] 신경망 구조 (0) | 2023.03.09 |
| [딥러닝 기초] 신경망 데이터 표현 (0) | 2023.03.08 |
| [딥러닝 기초] 신경망 기초수학 (0) | 2023.03.06 |