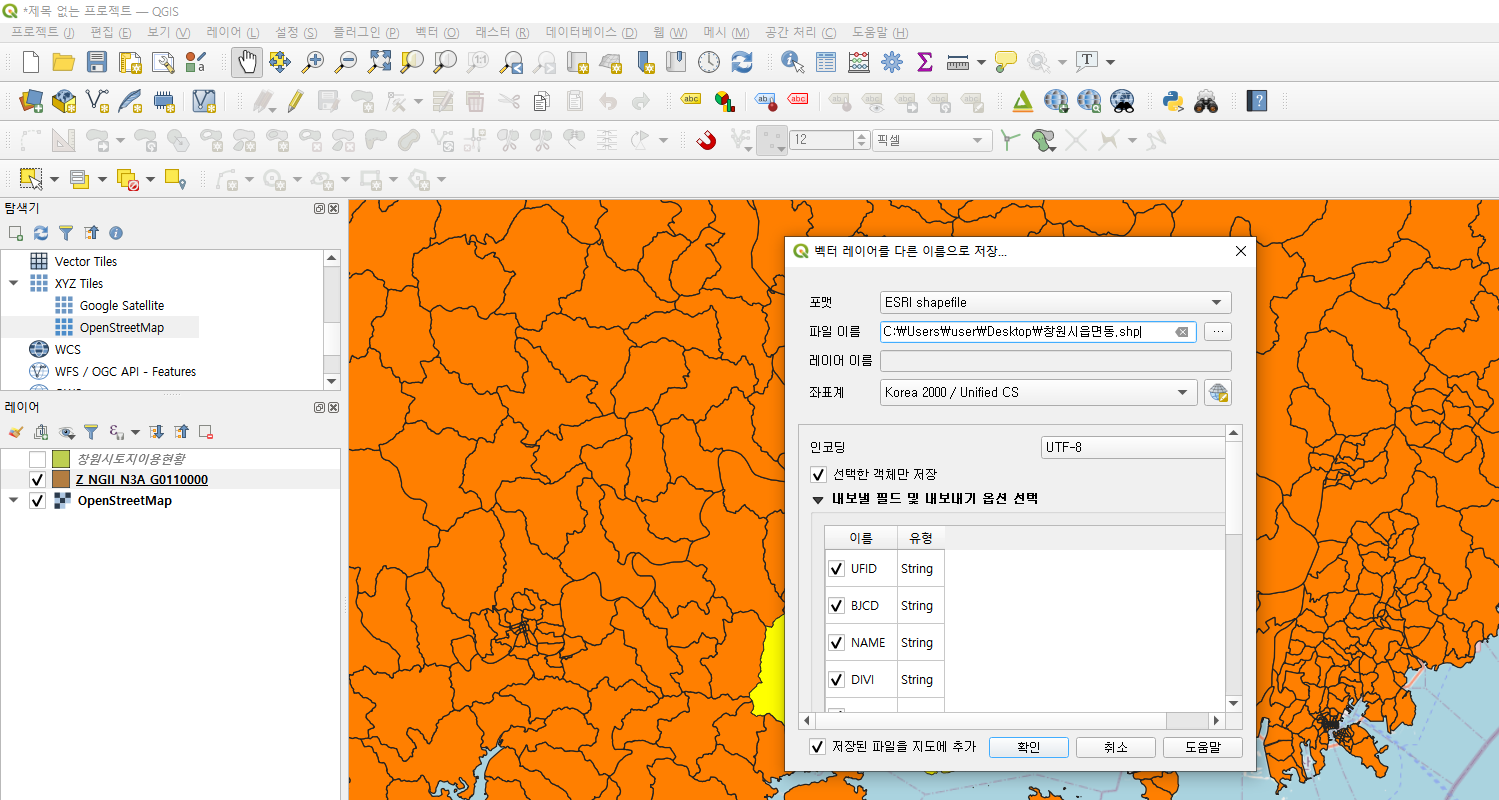
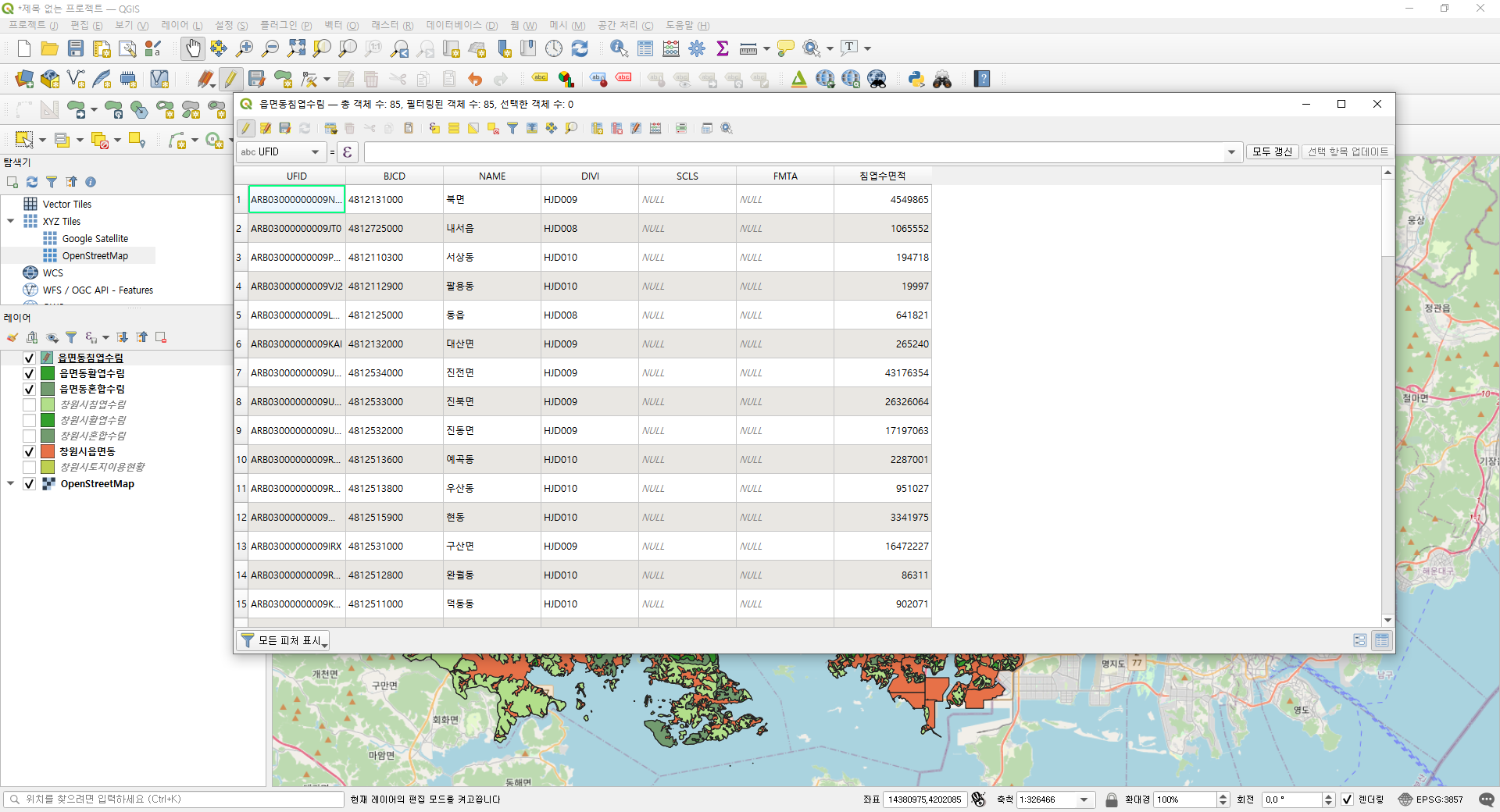
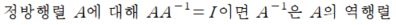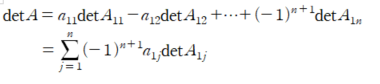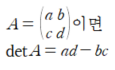1. 사용 데이터
-사이킷런에서 제공하는 MNIST 데이터셋(손글씨 데이터셋)
# 사이킷런에서 기본적으로 제공하는 MNIST 데이터셋 불러오기
from sklearn.datasets import fetch_openml
mnist=fetch_openml('mnist_784',version=1,as_frame=False)
mnist.keys()
### 결과 ###
dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])
-MNIST 데이터셋 배열 확인
X,y=mnist['data'],mnist['target']
X.shape # (70000, 784)
y.shape # (70000,)
# 이미지가 70000개이고 각 이미지는 784개의 특성을 가짐(28*28 픽셀의 이미지이므로 28*28=784개의 특성을 가짐)
# 각 특성은 0(흰색)~255(검은색)까지의 픽셀 강도
2. 다중 분류기 훈련
-서포트 벡터 머신(SVC) 분류기 사용
from sklearn.svm import SVC
svm_clf=SVC()
svm_clf.fit(X_train, y_train)
svm_clf.predict([some_digit])
### 결과 ###
array([5], dtype=uint8)
# 이진 분류기에서 5인지 아닌지에 따라 True, False로 결과가 나온 것과 달리 0~9까지 숫자 중 5라고 분류해냄
-점수 확인하기
-0~9까지 각 레이블에 대한 점수를 계산하여 가장 높은 점수를 가진 레이블로 예측함
-레이블이 5일때 가장 높은 점수일 것으로 예상
some_digit_scores=svm_clf.decision_function([some_digit])
some_digit_scores
### 결과 ###
array([[ 1.72501977, 2.72809088, 7.2510018 , 8.3076379 , -0.31087254,
9.3132482 , 1.70975103, 2.76765202, 6.23049537, 4.84771048]])-5일때 9.31점으로 가장 높은 점수가 나와 분류 결과가 5로 출력됨
-분류한 모든 클래스 출력하기
svm_clf.classes_
### 결과 ###
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)
-OvO(OneVsOneClassifier): 0과1 구별, 1과 2 구별..과 같이각 숫자 조합마다 이진 분류를 통해 분류기를 훈련시킴(N*(N-1)/2 개의 분류기 필요)
-OvR(OneVsRestClassifier): 모든 숫자를 훈련시킨 후, 가장 점수가 높은 것을 선택
-서포트 벡터 머신 같은 일부 알고리즘에서는 큰 훈련세트에서 몇 개의 분류기를 훈련시키는 것보다는 작은 훈련세트에서 많은 분류기 훈련시키는 것 선호
-이진 분류 알고리즘에서는 대부분 OvR 선호
-OvO나 OvR 강제로 사용하기
# OvO나 OvR 사용을 강제하려면 OneVsOneClassifier나 OneVsRestClassifier 사용
from sklearn.multiclass import OneVsRestClassifier
ovr_clf=OneVsRestClassifier(SVC())
ovr_clf.fit(X_train, y_train)
ovr_clf.predict([some_digit])
### 결과 ###
array([5], dtype=uint8)
# SGD 분류기는 직접 샘플을 다중 클래스로 분류할 수 있으므로 별도로 OvO 또는 OvR 적용할 필요 없음
# SGDClassifier 훈련
from sklearn.linear_model import SGDClassifier
sgd_clf=SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train)
sgd_clf.predict([some_digit])
### 결과 ###
array([3], dtype=uint8)
sgd_clf.decision_function([some_digit])
### 결과 ###
array([[-31893.03095419, -34419.69069632, -9530.63950739,
1823.73154031, -22320.14822878, -1385.80478895,
-26188.91070951, -16147.51323997, -4604.35491274,
-12050.767298 ]])-SGDClassifier에서 5를 3으로 분류해버림
-클래스마다 부여한 점수확인 결과 3에 부여한 점수가 1823으로 가장 높고 5에 부여한 점수는 그 다음으로 높은 -1385
# SGDClassifier의 성능 평가
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring='accuracy') # array([0.87365, 0.85835, 0.8689 ])
# 스케일 조정을 하면 정확도를 높일 수 있음
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
X_train_scaled=scaler.fit_transform(X_train.astype(np.float64))
cross_val_score(sgd_clf,X_train_scaled,y_train,cv=3,scoring='accuracy') # array([0.8983, 0.891 , 0.9018])
3. 에러 분석
-모델의 성능을 향상시키기 위해 에러의 종류를 분석하여 확인하는 것
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
y_train_pred=cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx=confusion_matrix(y_train, y_train_pred)
conf_mx
# 첫 행부터 실제 0일 때 0으로 예측한 개수, 1로 예측한 개수, 2로 예측한 개수...
-각 숫자를 정확히 예측한 개수가 가장 많지만 숫자 5에 대해 5로 예측한 횟수는 4444로 다른 숫자에 비해 낮음
-시각화 해보기
import matplotlib.pyplot as plt
plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()
-숫자 5부분만 조금 진한색으로 표시되어 다른 숫자들보다 정확히 예측해낸 횟수가 적음을 의미
-에러의 개수가 아닌 비율을 시각화해보기
-단순히 5의 전체 개수가 적어서 생긴 현상일 수 있으므로 전체 개수 대비 정확히 예측한 비율을 시각화
# 각 행의 합계 계산
row_sums=conf_mx.sum(axis=1,keepdims=True)
# 각 값을 행의 전체 합계로 나누어 비율 확인
norm_conf_mx=conf_mx / row_sums
# 대각원소는 0으로 채워 무시하고 나머지 값에서 에러 비율의 크기 확인
np.fill_diagonal(norm_conf_mx,0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()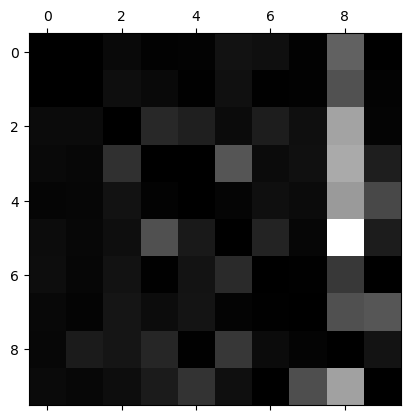
-8열이 밝은 것으로 보아 많은 이미지가 8로 잘못 분류됨
-3행 5열과 5행 3열이 밝은 것은 3과 5를 서로 잘못 분류한 비율이 높음을 의미
-3과 5에 대해 3을 3으로, 3을 5로, 5를 3으로, 5를 5로 예측한 데이터들을 한번에 살펴보기
# 그림 그리기 기능 함수
import matplotlib as mpl
def plot_digit(data):
image=data.reshape(28,28)
plt.imshow(image,cmap=mpl.cm.binary,interpolation='nearest')
plt.axis('off')
def plot_digits(instances, images_per_row, **options):
size=28
images_per_row=min(len(instances),images_per_row)
n_rows=(len(instances)-1) // images_per_row +1
# 필요하면 그리드의 끝을 채우기 위해 빈 이미지 추가
n_empty=n_rows*images_per_row-len(instances)
padded_instances=np.concatenate([instances, np.zeros((n_empty, size*size))],axis=0)
# 배열의 크기를 바꿔 28*28 이미지를 담은 그리드로 구성
image_grid=padded_instances.reshape((n_rows, images_per_row, size, size))
# 축 0(이미지 그리드의 수직축)과 2(이미지의 수직축)를 합치고 축 1과 3(그리드와 이미지의 수평축)을 합침
# transpose()를 통해 결합하려는 축을 옆으로 이동한 다음 합침
big_image=image_grid.transpose(0, 2, 1, 3).reshape(n_rows*size,images_per_row*size)
# 하나의 큰 이미지 출력
plt.imshow(big_image, cmap=mpl.cm.binary, **options)
plt.axis('off')
# 개개의 오류 살펴보며 왜 잘못되었는지 생각해보기(3과 5를 예시로)
cl_a, cl_b=3,5
X_aa=X_train[(y_train==cl_a) & (y_train_pred==cl_a)] # 실제 3을 3으로 예측
X_ab=X_train[(y_train==cl_a) & (y_train_pred==cl_b)] # 실제 3을 5로 예측
X_ba=X_train[(y_train==cl_b) & (y_train_pred==cl_a)] # 실제 5를 3으로 예측
X_bb=X_train[(y_train==cl_b) & (y_train_pred==cl_b)] # 실제 5를 5로 예측
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5) # X_aa에 해당하는 데이터를 처음 25개만 불러와서 5행으로 정렬
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5) # X_ab에 해당하는 데이터를 처음 25개만 불러와서 5행으로 정렬
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5) # X_ba에 해당하는 데이터를 처음 25개만 불러와서 5행으로 정렬
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5) # X_bb에 해당하는 데이터를 처음 25개만 불러와서 5행으로 정렬
plt.show()
-5를 3으로 잘못 예측해낸 것(제3사분면) 중 첫 행 2열은 사람이 봐도 3같을 정도로 잘못 분류할 확률이 높아보임
-위 방식으로 에러를 확인하여 어디서, 왜 오차가 나는지 확인하고 해결방법 고안하기
ex) 3과 5는 위의 선분과 아래의 원을 잇는 수직선의 위치가 왼쪽, 오른쪽으로 다르다는 점 등을 이용하여 다시 학습시키기
4. 다중 레이블 분류
-분류해내야 하는 타겟변수가 여러 개일 때, 여러 개를 한 번에 분류
-KNeighborsClassifier, DecisionTreeClassifier, RandomForestClassifier, OneVsRestClassifier에서 다중 분류 지원
from sklearn.neighbors import KNeighborsClassifier
y_train_large=(y_train>=7) # 분류한 결과가 7보다 큰지
y_train_odd=(y_train%2==1) # 분류한 결과가 홀수인지
y_multilabel=np.c_[y_train_large,y_train_odd] # 위의 두 개의 사항에 대해 예측하는 다중 레이블
knn_clf=KNeighborsClassifier()
knn_clf.fit(X_train,y_multilabel)
knn_clf.predict([some_digit]) # 숫자 5에 대해 예측결과 반환
### 결과 ###
array([[False, True]])
# f1_score를 통해 얼마나 정확한지 확인
from sklearn.metrics import f1_score
y_train_knn_pred=cross_val_predict(knn_clf,X_train,y_multilabel,cv=3)
f1_score(y_multilabel, y_train_knn_pred,average='macro')
### 결과 ###
0.976410265560605-숫자 5를 7보다 크지 않고,(False), 홀수(True)라고 정확히 분류해냄
5. 다중 출력 분류
-다중 레이블 분류에서 한 레이블이 값을 두 개이상 가질 수 있는 분류
-MNIST 숫자 이미지 데이터는 한 픽셀당 한 레이블이므로 레이블이 784개인 다중 레이블임
-각 레이블은 0~255까지의 숫자를 가질 수 있는 다중 출력 분류가 가능한 데이터셋임
# MNIST 이미지의 픽셀 강도에 잡음 추가
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise # 독립변수는 잡음이 섞인 데이터
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train # 예측해야하는 변수는 원래 데이터
y_test_mod = X_test
some_index = 5500
plt.subplot(121); plot_digit(X_test_mod[some_index])
plt.subplot(122); plot_digit(y_test_mod[some_index])
plt.show()
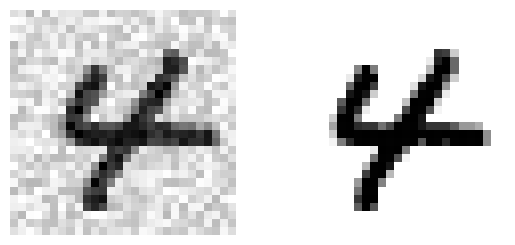
-좌측은 노이즈를 섞은 데이터로 훈련기에 넣으면 노이즈를 제거하여 원래 이미지를 예측해낼 것
-우측은 원래의 이미지
knn_clf.fit(X_train_mod,y_train_mod)
clean_digit=knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)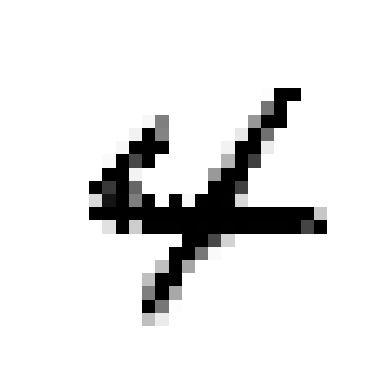
-노이즈가 있던 왼쪽의 이미지를 분류기에 넣어 분류기가 원래 이미지를 분류해낸 모습
'Python > Machine Learning' 카테고리의 다른 글
| [머신러닝 알고리즘] 사이킷런 제대로 시작하기(2) (0) | 2022.12.28 |
|---|---|
| [머신러닝 알고리즘] 사이킷런 제대로 시작하기(1) (1) | 2022.12.26 |
| [ML] 모델 훈련 (1) - 선형회귀 (0) | 2022.10.31 |
| [ML] 분류 (1) - 이진 분류 (0) | 2022.10.26 |
| [ML] 머신러닝 프로젝트의 베이스라인 (0) | 2022.10.25 |